Funktio
Funktio eli kuvaus kertoo olioiden välisistä riippuvuussuhteista.[1] [2]
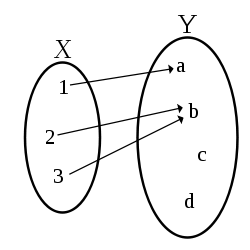
Formaalisti funktio joukolta joukkoon on sääntö, joka liittää jokaiseen joukon alkioon täsmälleen yhden joukon alkion. Funktiota merkitään yleensä symbolilla .
Funktioon liittyviä joukkoja kutsutaan :n lähtö- eli määrittelyjoukoksi () ja maalijoukoksi (). Jos , niin sanotaan, että on joukon funktio. Määrittelyjoukon alkioita kutsutaan usein funktion argumenteiksi. Sitä, että :n argumenttiin liittämä arvo on , merkitään yleensä , eli funktion kuva-alkio. Tämän merkinnän otti käyttöön Leonhard Euler vuonna 1734.[3] Esimerkiksi asetetaan kuvitellussa tilanteessa :n määrittelyjoukoksi nelihenkinen perhe. on nyt siis ihminen-tyyppisistä alkioista koostuva joukko, jossa on neljä alkiota. Asetetaan sitten maalijoukoksi kaikkien mahdollisten suomalaisten etunimien joukko. Koska jokaiseen ihmiseen voimme liittää jonkin yksikäsitteisen etunimen, niin voimme muodostaa funktion nelihenkisen perheen ja kaikkien etunimien joukon välille. Tämän funktion argumentit ovat perheenjäseniä ja arvot perheenjäsenten etunimet.
Matematiikassa ja sen sovelluksissa tavallisin funktiotyyppi on sellainen, jossa lähtö- ja maalijoukot ovat lukujoukkoja ja funktion määrittelevä vastaavuus voidaan ilmaista laskutoimituksin. Tällöin on tavallista, joskin muodollisesti epäkorrektia, nimetä funktio määrittelyjoukon yleiseen alkioon kohdistuvan laskutoimituksen osoittavalla kaavalla, esimerkiksi "funktio ".
Esimerkkejä yleisestä määritelmästä
muokkaa, jolla , on funktio reaalilukujen joukossa. Tässä funktio liittää jokaiseen reaalilukuun luvun itsensä, ks. Identtinen funktio.
, jolla . Nyt funktio liittää jokaiseen reaalilukuun tämän luvun neliön.
, jolla , on kahden muuttujan funktio (ks. alla). Funktio liittää jokaiseen reaalilukupariin lukujen neliöiden summan.
Tarkka määritelmä
muokkaaYleensä edellä annettu määritelmä riittää pitkällekin menevissä matematiikan tutkimuksissa ja sovelluksissa. Kuitenkin on tarpeellista joskus määritellä funktio täsmällisemmin kuin lausein ja sanoin. Olkoot jälleen ja joukkoja. Tällöin näiden karteesisen tulon osajoukko on funktio, jos sille pätevät ehdot
ja
Toisin sanoen pari on funktion alkio, jos ja vain jos jokaisella kuva-alkiosta poikkeavilla alkioilla pari ei ole funktion alkio. Siispä funktiossa kukin joukon alkio esiintyy tarkalleen kerran funktion parin ensimmäisenä alkiona. Funktio on siis erikoistapaus yleisemmistä kaksipaikkaisista relaatioista. Eksaktin määritelmän avulla funktiot ja ovat samat, kun ne ovat sama joukko, eli pätee .
Esimerkkejä eksaktista määritelmästä
muokkaaOlkoon joukko ja joukko . Nyt näiden karteesinen tulo on joukko .
Funktiot joukossa ovat osajoukot:
- eli
- eli
- eli
- eli
- eli
- eli
- eli .
Funktion kuvaaja
muokkaaFunktiota on yleensä tapana mahdollisuuksien puitteissa kuvata myös visuaalisesti. Tämän mahdollistaa funktion kuvaajan käsite. Täsmällisesti jos on funktio, niin sen kuvaaja on karteesisen tulon osajoukko
Funktion kuvaaja koostuu siis määrittelyjoukon alkion ja vastaavan arvojoukon alkion muodostamista pareista. Funktion kuvaajan määritelmä on identtinen yllä esitetyn funktion eksaktin määritelmän kanssa.
Esimerkiksi funktion , kuvaaja on määritelmän mukaan karteesisen tulon osajoukko
Tässä tapauksessa koska joukko on tavallinen 2-ulotteinen euklidinen avaruus , niin voidaan funktion kuvaajaa hahmottaa visuaalisesti sijoittamalla tasoon kuvaaja-joukon pisteet kuten oheisessa kuvassa näkyy.
Yhdistetty funktio
muokkaaJos , ja , niin on määriteltävissä funktio siten, että . Funktio on funktioista ja yhdistetty funktio ja sitä merkitään . Merkintä luetaan "g pallo f".
Jos esimerkiksi , ja , niin ja .
Vektorimuuttujan funktiot ja vektoriarvoiset funktiot
muokkaaKun funktion lähtöjoukko on hahmotettavissa useamman joukon karteesiseksi tuloksi, on usein tapana puhua usean muuttujan funktiosta tai vektorimuuttujan funktiosta. Jos , niin funktion alkioon liittämää kuva-alkiota merkitään yleensä . Esimerkiksi ilmanpaine tietyssä paikassa ja tietyllä hetkellä on neljän muuttujan (kolme paikkakoordinaattia ja aika) reaaliarvoinen funktio . Tutumpi esimerkki on yhteenlaskufunktio : lukuparin yksikäsitteinen kuva-alkio on lukujen ja summa, ja sitä merkitään yksinkertaisemmin (ks. Laskutoimitus).
Vastaavasti funktion palauttama arvo voi olla usean joukon karteesisen tulon alkio. Tällöin on tapana puhua vektoriarvoisesta funktiosta. Esimerkiksi joen virtaussuunta tasokartalla ja nopeus (kaksi arvoa) voidaan ilmoittaa joen suulta mitatun etäisyyden funktiona , missä on jokin vakio . Erityisesti fysiikassa vektoriarvoisen funktion sijasta puhutaan yleensä vektorikentästä. Esimerkiksi sähkökenttää voi kuvata funktio, joka liittää tiettyyn paikka- ja aika-avaruuden pisteeseen kentän suunnan, eli kyseessä on kuvaus .
Joukkojen kuvat ja alkukuvat
muokkaaOlkoon funktio eli kuvaus.
- Joukon kuvajoukko eli kuva kuvauksessa on joukko
Toisinaan kuvajoukkoa merkitään ilman sulkeita: . Funktion kuvajoukko on siis maalijoukon osajoukko ja se koostuu niistä :n kuva-alkioista, joille määrittelyjoukon osajoukon alkiot kuvautuvat kuvauksessa . Jos asetamme osajoukoksi koko määrittelyjoukon , ei välttämättä vastaava kuvajoukko ole koko maalijoukko . Esimerkiksi funktion , , määrittelyjoukon kuva , joka on maalijoukon aito osajoukko.
- Joukon alkukuva kuvauksessa on joukko
Funktion alkukuva on siis määrittelyjoukon osajoukko ja se koostuu niistä :n alkioista, jotka kuvautuvat joukon alkioille kuvauksessa . Yksittäisen alkion alkukuva on . Jos asetetaan osajoukoksi koko maalijoukko , niin vastaava alkukuva on koko määrittelyjoukko. Koko määrittelyjoukko voi kuitenkin olla jonkin maalijoukon aidon osajoukon alkukuva. Esimerkiksi funktion , , maalijoukon osajoukon alkukuva on eli koko määrittelyjoukko.
Alkeisfunktiot
muokkaaMatematiikassa ja sen sovelluksissa tavallisimpia reaalimuuttujan funktioita kutsutaan alkeisfunktioiksi. Alkeisfunktioita ovat ensinnäkin polynomit eli funktiot, jotka määritellään muuttujasta ja vakioista yhteen- ja kertolaskun avulla muodostetuilla laskulausekkeilla. Polynomifunktion yleinen muoto on
Polynomifunktioiden erikoistapauksia ovat vakiofunktiot , missä on jokin vakio, ja identtinen (reaalimuuttujan) funktio . Rationaalifunktiot määritellään lausekkein, joissa voi esiintyä yhteen- ja kertolaskun lisäksi myös jakolaskuja. Rationaalifunktion laskulauseke voidaan aina saattaa muotoon
eli kahden polynomifunktion osamaaräksi. Koska nimittäjä voi olla nolla, rationaalifunktion määrittelyjoukko ei yleensä voi olla koko reaalilukujen joukko. Kun funktion lausekkeen muodostamisessa saa käyttää myös juurenottoja, funktio on algebrallinen funktio.
Algebrallisten funktioiden lisäksi alkeisfunktioihin luetaan eksponenttifunktiot, logaritmifunktiot, trigonometriset funktiot käänteisfunktioineen ja kaikki näistä yhdistämällä muodostetut funktiot.
Funktion ydin ja kantaja
muokkaaAlgebrassa voidaan funktioille lisäksi määritellä ytimen käsite, joka on osoittautunut esimerkiksi isomorfisuuden tutkimisessa hyödylliseksi välineeksi.
Olkoon seuraavassa G ja G´ ryhmiä ja jokin funktio.
- Funktion ydin on joukko
missä merkintä tarkoittaa arvojoukon nolla-alkiota. Toisin sanoen funktion ydin koostuu niistä määrittelyjoukon alkioista, jotka kuvautuvat nolla-alkiolle. Funktion ydin on siis erityisesti nolla-alkion muodostaman yksiön alkukuva. Esimerkiksi funktion , , ydin koostuu pelkästä luvusta 0 sillä jos ja vain jos .
Erityisesti funktionaalianalyysissä hyödyllinen käsite on funktion kantaja. Jos funktion määrittelyjoukko on topologinen avaruus ja arvojoukko on reaali- tai kompleksilukujen joukko, funktion kantaja on joukon ( ) sulkeuma eli pienin kyseisen joukon sisältävä suljettu joukko.
Funktiokäsitteen historiaa
muokkaaSanan funktio etymologia perustuu latinan verbiin fungi, 'tehdä, toimia, toimittaa'. Sanaa sen matemaattisessa merkityksessä käytti ensimmäisenä saksalainen G. W. Leibniz vuonna 1694. Sveitsiläinen Johann Bernoulli käytti vuonna 1718 merkintää . Merkintää käyttivät ensi kerran ranskalainen Alexis Claude Clairaut (1713–1765) ja sveitsiläinen Euler vuonna 1734. Funktiolla ymmärrettiin pitkään laskulausekkeen tulosta, mutta jo Eulerilla esiintyy ajatus funktiosta minä hyvänsä lukujen välisenä yhteytenä. Saksalainen Dirichlet esitti vuonna 1837 olennaisesti nykyisen funktion määritelmän, joka ei sido funktiota lukujen laskutoimituksiin.
Erityisesti Cauchyn, Riemannin ja Weierstrassin havainnot kompleksilukumuuttujan kompleksilukuarvoisista funktioista synnyttivät 1800-luvulla funktioteoriaksi kutsutun matematiikan osa-alueen. Sen tutkimus on ollut elinvoimaista Suomessa 1900-luvulla.
Funktion ominaisuuksia
muokkaaFunktiolle on määritelty paljon erilaisia ominaisuuksia:
Katso myös
muokkaaLähteet
muokkaa- ↑ Pekka Kontkanen, Riitta Liira, Kerkko Luosto, Juha Nurmi, Riikka Nurmiainen, Anja Ronkainen ja Sisko Savolainen: Pyramidi 1, s. 115. Kustannusosakeyhtiö Tammi, 2010. ISBN 978-951-26-5134-4.
- ↑ Häsä, Jokke; Rämö, Johanna: Johdatus abstraktiin algebraan, s. 18–19. Helsinki: Gaudeamus, 2015. ISBN 978-952-495-361-0.
- ↑ Leonhard Euler - Biography Maths History. Viitattu 5.12.2021. (englanniksi)
Kirjallisuutta
muokkaa- Häsä, Jokke; Rämö, Johanna: Johdatus abstraktiin algebraan. Helsinki: Gaudeamus, 2015. ISBN 978-952-495-361-0.
- Merikoski, Jorma; Virtanen, Ari; Koivisto, Pertti: Diskreetti matematiikka I. Tampere: Tampereen yliopisto, 2001 (1993). ISBN 951-44-3604-0.
- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).
Aiheesta muualla
muokkaa- Kuvia tai muita tiedostoja aiheesta Funktio Wikimedia Commonsissa













