Särmiö

Tämä artikkeli kertoo geometrisesta kappaleesta. Särmiöt on kasvisuku.

Uniformiset särmiöt
(Kuvassa kuusikulmainen särmiö)
Tyyppi	Uniforminen monitahokas
Conwayn monitahokas- merkintä	Pn
Tahkoja	2+n yhteensä: 2 {n} n Neliö\|{4}
Särmiä	3n
Kärkiä	2n
Schläflin symboli	{n}×{}^[1] tai t{2, n}
Coxeterin diagrammi
Kärkikonfiguraatio	4.4.n
Symmetriaryhmä	D_nh, [n,2], (*n22), kertaluku 4n
Rotaatioryhmä	D_n, [n,2]⁺, (n22), kertaluku 2n
Duaalikappale	Bipyramidit
Ominaisuuksia	kupera, semiregulaarinen, särmätransitiivinen
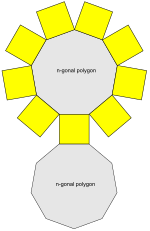n-kulmainen särmiöverkko (tässä n = 9)]]

Särmiö eli prisma^[2] on geometriassa monitahokas, jonka tahkoina on kaksi keskenään yhtenevää monikulmiota, joiden vastaavat sivut ovat yhdensuuntaiset, sekä joukko suunnikkaita, jotka yhdistävät nämä monitahokkaat toisiinsa.^[3] Näitä yhdensuuntaisia monitahokkaita sanotaan särmiön pohjiksi, niitä yhdistäviä suunnikkaan muotosia tahkoja särmiön sivutahkoiksi. Sivutahkot yhdessä muodostavat särmiön vaipan.^[3] Särmiön kaikki leikkauspinnat pohjan kanssa yhdensuuntaisten tasojen kanssa ovat pohjien kanssa yhteneviä ja siitä yhdensuuntaissiirrolla muodostettavia. Särmiötä nimitetään sivutahkojen lukumäärän mukaan, joka on samalla pohjan sivujen lukumäärä.^[2] Esimerkiksi särmiötä, jonka pohja on viisikulmio, sanotaan viisikulmaiseksi särmiöksi. Särmiöt muodostavat osajoukon prismatoideista.

Yleiset, suorat ja uniformiset särmiöt muokkaa

Suora särmiö on särmiö jonka pohjia yhdistävät särmät ja tahkot ovat kohtisuorassa pohjatahkoja vastaan. Suoran särmiön muut tahkot paitsi mahdollisesti pohjat ovat suorakulmioita.^[4] Suoraa särmiötä, jonka pohjat ovat säännöllisiä monikulmiota, sanotaan säännölliseksi särmiöksi.^[3] Suoraa särmiötä, jonka pohjat ovat säännöllisiä p-kulmioita, voidaan merkitä Schläflin symbolilla { } × {p}.

Jos yhdistävät tahkot ja sivut eivät ole kohtisuorassa pohjiin nähden, särmiötä sanotaan vinoksi särmiöksi.

Särmiötä, jonka pohjakin on suunnikas, sanotaan suuntaissärmiöksi eli parallelepipediksi.^[2]. Suuntaissärmiö on monitahokas, jonka kaikki kuusi tahkoa ovat suunnikkaita.

Suoraa särmiötä, jonka pohja on suorakulmio, sanotaan suorakulmaiseksi särmiöksi.^[2] Sellaisen Schläflin symboli on { } × { } × { }. Jos pohja on neliö ja jos lisäksi pohjien välinen etäisyys on yhtä suuri kuin tämän neliön sivu, kyseessä on kuutio^[2], joka kuuluu samalla myös säännöllisiin monitahokkaisiin.^[5]

Nimitystä uniforminen tai semiregulaarinen särmiö käytetään sellaisista särmiöistä, joiden sivutahkot ovat neliöitä, sillä ne kuuluvat myös uniformisten monitahokkaiden joukkoon. Uniformisen p-kulmaisen särmiön Schläflin symboli on t{2,p}. Esimerkiksi kuutio on uniforminen 4-kulmainen särmiö. Suorat särmiöt, joilla on säännölliset pohjat ja yhtä pitkät särmät, muodostavat toisen kahdesta äärettömästä semiregulaaristen monitahokkaiden sarjasta; toisen tällaisen sarjan muodostavat antiprismat.

Katkaistu kolmikulmainen prisma, jonka ylin tahko on katkaistu vinossa kulmassa.

Suoran särmiön duaalikappale on bipyramidi.

Särmiöt voidaan käsittää myös lieriön alalajiksi, joissa pohja on monikulmio.^[6] Särmiöt, joiden pohjana on säännöllinen n-kulmio, lähestyvät muodoltaan ympyräpohjaista lieriötä, kun n kasvaa rajatta.

Katkaistu särmiö on särmiötä muistuttava monitahokas, jonka pohjat kuitenkaan eivät ole yhdensuuntaisia.^[7]

Tilavuus muokkaa

Särmiön tilavuus on sen pohjan pinta-alan ja pohjien välisen etäisyyden eli särmiön korkeuden tulo. Jos särmiö ei ole suora, tässä tarkoitetaan kohtisuoraa etäisyyttä.

Särmiön tilavuus on siis^[4]

V=Bh

missä B on sen pohjan pinta-ala ja h sen korkeus. Jos särmiön pohjana on säännöllinen n-kulmio, jonka sivun pituus on s, särmiön tilavuus on:

V={\frac {n}{4}}hs^{2}\cot({\frac {\pi }{n}})

Pinta-ala muokkaa

Särmiön kaikkien tahkojen yhteenlaskettu pinta-ala on

2B+Ph

missä B on sen pohjan pinta-ala, h sen korkeus ja P pohjan ympärysmitta.

Jos suoran särmiön pohjana on säännöllinen n-kulmio, jonka sivun pituus on s, ja särmiön korkeus on h, sen kaikkien tahkojen yhteenlaskettu pinta-ala on

A={\frac {n}{2}}s^{2}\cot {\frac {\pi }{n}}+nsh

Schlegelin diagrammit muokkaa

Särmiöt, joiden pohjana on säännöllinen monikulmio, voidaan kuvata Schlegelin diagrammeina seuraavaan tapaan:

P3	P4	P5	P6	P7	P8

Symmetria muokkaa

Sellaisen suoran särmiön symmetriaryhmä, jonka pohjana on n-sivuinen säännöllinen monikulmio, on kertaluvun 4n diedriryhmä D_nh. Poikkeuksena on kuutio, jolla on laajempi symmetriaryhmä, kertaluvun 48 oktaedrinen symmetriaryhmä O_h, johon sisältyy aliryhmänä kolme versiota ryhmästä D_4h. Tällaisen särmiön rotaatioryhmä on D_n kertalukua 2n, paitsi kuutiolla, jolla on laajempi kertaluvun 24 symmetriaryhmä O ja sillä aliryhminä kolme versiota ryhmästä D₄.

Peilaus särmiön keskipisteen suhteen kuuluu symmetriaryhmään D_nh, jos ja vain jos n on parillinen.

Prismaattiset polytoopit muokkaa

Prismaattinen polytooppi on prisman eli särmiön korkeampiulotteinen yleistys. Prismaattinen n-polytooppi on n-ulotteinen polytooppi, joka muodostetaan kahdesta n - 1)-ulotteisesta polytoopista, jotka saadaan toisistaan yhdensuuntaissiirrolla seuraavassa ulottuvuudessa.

Prismaattisen n-polytoopin elementit saadaan kaksinkertaistamalla (n - 1)-polytoopin elementit ja luomalla uudet elementit lähinnä alemmasta elementistä.

Oletetaan n-polytooppi, jossa on f_i i-tahkoa (i = 0, ..., n). Siitä voidaan muodostaa prismaattinen (n + 1)-polytooppi, jossa on 2f_i + f_i-1 i-tahkoelementtiä. (Kun f_-1 = 0, saadaan f_n = 1.)

Eri ulottuvuuksissa:

Lähtemällä monikulmiosta, jossa on n kärkeä ja n sivua, voidaan konstruoida särmiö eli prismaattinen 3-polytooppi, jossa on 3n särmää ja 2 + n tahkoa.
Lähtemällä monitahokkaasta, jossa on v kärkeä, e särmää ja f tahkoa, voidaan konstruoida prismaattinen 4-polytooppi, jossa on 2v kärkeä, 2e + v särmää, 2f + e tahkoa ja 2 + f solua.
Lähtemällä polykoorista, jossa on v kärkeä, e särmää, f tahkoa ja c solua, voidaan konstruoida prismaattinen 5-polytooppi, jossa on 2v kärkeä, 2e + v särmää, 2f + e tahkoa, 2c + f solua ja 2 + c hypersolua.

Uniforminen prismaattinen polytooppi muokkaa

Säännöllisestä n-polytoopista, jota esittää Schläflin symboli {p, q, ..., t}, voidaan muodostaa uniforminen prismaattinen (n + 1)-polytooppi, jota esittää kahden Schläflin symbolin karteesinen tulo: {p, q, ..., t}×{}.

Ulottuvuuksittain:

0-polytooppinen särmiö on jana, jota esittää tyhjä Schläflin symboli {}.
1-polytooppinen särmiö on suorakulmio, joka muodostetaan yhdensuuntaissiirrolla kahdesta janasta. Se voidaan esittää Schläflin symbolilla {}×{}. Jos se on neliö, sen symmetria voidaan esittää myös muodossa {}×{} = {4}.
Polygonaalinen särmiö on 3-ulotteinen särmiö, joka saadaan kahdesta yhdensuuntaissiirrolla toisilleen kuvattavasta monikulmiosta joita yhdistävät suorakulmiot. Säännöllisestä monikulmiosta {p} voidaan konstruoida uniforminen n-kulmainen särmiö, jota esittää tulo {p}×{}. Jos p = 4, tuloksena saadaan kuutio: {4}×{} = {4, 3}.
Polyedraalinen särmiö on 4-ulotteinen prismaattinen polytooppi, joka saadaan kahdesta yhdensuuntaisesta särmiöstä yhdistämällä ne kolmiulotteisilla särmiösoluilla. Säännöllisestä monitahokkaasta {p, q} voidaan konstruoida uniforminen polykoorinen prisma, jonka Schläflin symboli on {p, q}×{}. Jos sekä lähtökohtana oleva monitahokas että sivuina olevat monitahokkaat ovat kuutioita, tuloksena saadaan tesserakti: {4, 3}×{} = {4, 3, 3}.
...

Korkeamman kertaluvun prismaattisia polytooppeja saadaan myös minkä tahansa kahden polytoopin karteesisina tuloina. Polytoopin ulottuvuus on sen elementtien ulottuvuuksien tulo. Ensimmäisinä esimerkkeinä näistä ovat 4-ulotteisen avaruuden duoprismat, jotka saadaan kahden monikulmion karteesisina tuloina. Säännöllisiä duoprismoja esittävät Shcläflin symbolit ovat muotoa {p}×{q}.

Uniformiset särmiöt
Coxeter
Monitahokas
Laatoitus
Särmäkonfiguraatio.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4

Väännetty särmiö muokkaa

Väännetty särmiö (engl. Twisted prism) on ei-kupera särmiötä muistuttava monikulmio, joka voidaan konstruoida uniformisesta q-särmiöstä katkaisemalla sen sivutahkot neliön lävistäjillä ja kiertämällä ylempää pohjaa, tavallisesti ${\frac {\pi }{q}}$ radiaania ( ${\frac {180}{q}}$ astetta) samaan suuntaan, niin että sivukolmioista tulee koveria.^[8]^[9]

Väännettyä särmiötä ei voi jakaa tetraedreiksi lisäämättä siihen uusia kärkiä. Pienintä tapauksta, jossa pohjat ovat kolmiota, sanotaan Schönhardtin monitahokkaaksi.

Väännetty prisma on topologisesti antiprisman kaltainen, mutta sillä on vain puolet antiprisman symmetriasta: D_n, [n,2]⁺, kertalukua 2n. Sitä voidaan pitää kuperana antiprismana, josta on poistettu kolmioparien väliset tetraedrit.

3-kulmainen	4-kulmainen		12-kulmainen
Schönhardtin monitahokas	Väännetty neliösärmiö	Neliön antiprisma	Väännetty 12-kulmainen antiprisma

Katkaistut pyramidit muokkaa

Viisikulmainen katkaistu pyramidi

Katkaistut pyramidit ovat topologisesti täysin särmiöiden kaltaisia eli niiden kanssa homeomorfisia, mutta niiden sivutahkot ovat puolisuunnikkaita ja pohjat yhdenmuotoisia mutta eri kokoisia monikulmioita.

Tähtisärmiöt muokkaa

Tähtisärmiö on ei-kupera monitahokas, jonka konstruoidaan asettamalla pohjiksi kaksi keskenään yhtenevää ja yhdensuuntaista tähtimonikulmiota, jotka ovat avaruudessa tietyllä etäisyydellä toisistaan. Uniformisen tähtimonikulmion Schläflin symboli on {p/q} × { }, kun sillä on sivutahkoina p suorakulmiota sekä kaksi tähtimonikulmion muotoista tahkoa, joiden Schläflin symboli on {p/q}. Se on topologisesti p-kulmaisen särmiön kaltainen.

Esimerkkejä
{ }×{ }₁₈₀×{ }	t_a{3}×{ }		{5/2}×{ }	{7/2}×{ }	{7/3}×{ }	{8/3}×{ }
D_2h, order 8	D_3h, order 12		D_5h, order 20	D_7h, order 28		D_8h, order 32

Käännös suomeksi

Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Prism (geometry)

Lähteet muokkaa

Anthony Pugh: ”Archimedean polyhedra, prisma ana antiprisms”, Polyhedra: A visual approach. University of California Press Berkeley, 1976. ISBN 0-520-03056-7.

Viitteet muokkaa

↑ Norman Johnson: ”Finite symmetry groups: Pyramids, Prisms and Antiprisms, kuva 11.3b”, Geometries and Transformations. Cambridge University Press Vuosi = 2018. ISBN 978-1-107-10340-5. Teoksen verkkoversio.
↑ ^a ^b ^c ^d ^e Kalle Väisälä: ”Tärkeimmät kappaleet ja niiden tilavuudet ja pinta-alat”, Geometria, s. 61. WSOY, 1959. Teoksen verkkoversio.
↑ ^a ^b ^c ”Särmiö”, Otavan iso Fokus, 7. osa (Sv–Öö), s. 4146. Otava, 1974. ISBN 951-1-01521-4.
↑ ^a ^b Prism Wolfram MathWorld. Eric W. Weisstein. Viitattu 15.11.2018.
↑ Kalle Väisälä: ”Säännölliset monitahokkaat”, Geometria, s. 157. WSOY, 1959. Teoksen verkkoversio.
↑ Esko Ranta, Salme-Laura Leikkonen: ”Lieriöt ja särmiöt”, Geometria, s. 123. WSOY, 1971.
↑ William F. Kern, James R. Bland: Solid Mensuration with proofs, s. 81. {{{Julkaisija}}}, 1938.
↑ Catherine A. Gorini: The facts on file: Geometry handbook, s. 172. Checkmark Books, 2003. ISBN 0-8160-4875-4.
↑ ms Pictures of Twisted Prisms Gijs Korhals Altes. Viitattu 15.11.2018.

Aiheesta muualla muokkaa

Kuvia tai muita tiedostoja aiheesta Särmiö Wikimedia Commonsissa

[1] Norman Johnson: ”Finite symmetry groups: Pyramids, Prisms and Antiprisms, kuva 11.3b”, Geometries and Transformations. Cambridge University Press Vuosi = 2018. ISBN 978-1-107-10340-5. Teoksen verkkoversio.

[Vaisala-2] Kalle Väisälä: ”Tärkeimmät kappaleet ja niiden tilavuudet ja pinta-alat”, Geometria, s. 61. WSOY, 1959. Teoksen verkkoversio.

[Fokus-3] ”Särmiö”, Otavan iso Fokus, 7. osa (Sv–Öö), s. 4146. Otava, 1974. ISBN 951-1-01521-4.

[MathWorld-4] Prism Wolfram MathWorld. Eric W. Weisstein. Viitattu 15.11.2018.

[5] Kalle Väisälä: ”Säännölliset monitahokkaat”, Geometria, s. 157. WSOY, 1959. Teoksen verkkoversio.

[6] Esko Ranta, Salme-Laura Leikkonen: ”Lieriöt ja särmiöt”, Geometria, s. 123. WSOY, 1971.

[7] William F. Kern, James R. Bland: Solid Mensuration with proofs, s. 81. {{{Julkaisija}}}, 1938.

[8] Catherine A. Gorini: The facts on file: Geometry handbook, s. 172. Checkmark Books, 2003. ISBN 0-8160-4875-4.

[9] s Pictures of Twisted Prisms Gijs Korhals Altes. Viitattu 15.11.2018.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]