Normaalijakauma
Normaalijakauma (toisilta nimiltään Gaussin jakauma tai Gaussin kellokäyrä) on jatkuva todennäköisyysjakauma. Nimitys kellokäyrä tulee siitä, että tiheysfunktion kuvaaja muistuttaa kirkonkellon sivukuvaa. Luonnontieteissä normaalijakaumalle on paljon käytännöllisiä tulkintoja.
Tiheysfunktio Punainen kuvaaja on standardoitu normaalijakauma | |
Kertymäfunktio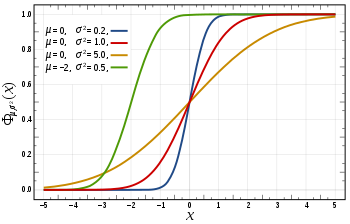
| |
| Merkintä | |
|---|---|
| Parametrit | μ ∈ R — keskiarvo (sijainti) σ2 > 0 — varianssi (neliöity skaala) |
| Määrittelyjoukko | x ∈ R |
| Tiheysfunktio | |
| Kertymäfunktio | |
| Odotusarvo | μ |
| Mediaani | μ |
| Moodi | μ |
| Varianssi | |
| Vinous | 0 |
| Huipukkuus | 0 |
| Entropia | |
| Momentit generoiva funktio | |
| Karakteristinen funktio | |
| Fisherin informaatiomatriisi | |
Normaalijakauma on määritelty ja jatkuva kaikilla muuttujan reaaliarvoilla. Jos satunnaismuuttuja on normaalijakautunut, niin merkitään
Parametri on jakauman odotusarvo ja on jakauman varianssi. Jakauman sijainti riippuu keskiarvoparametrista ja leveys varianssiparametrista. Jakauman tiheysfunktio on
Normaalijakauman kertymäfunktio on integraali
jota ei voida ratkaista analyyttisesti alkeisfunktioiden avulla. Kertymäfunktion arvoja voidaan kuitenkin laskea numeerisilla menetelmillä.
Standardoitu normaalijakauma eli standardinormaalijakauma on yleisen normaalijakauman erikoistapaus . Standardoidussa normaalijakaumassa jakauman odotusarvo on 0 ja varianssi 1. Useimmissa matematiikan taulukkokirjoissa on taulukoituna standardinormaalijakauman kertymäfunktion arvoja positiivisissa pisteissä. Normaalijakauman kertymäfunktion arvojen laskeminen numeerisesti on tarkempaa, mikäli jakauma on standardinormaalijakauma.[1]
Standardinormaalijakauman tapauksessa kertymäfunktio voidaan esittää myös siihen läheisesti liittyvän virhefunktion avulla seuraavasti:
Keskeisen raja-arvolauseen perusteella normaalijakaumalla on yhteys muihinkin jakaumiin. Tiettyjen lievien oletusten ollessa voimassa ja poimimalla riippumattomasti samasta jakaumasta suuri määrä satunnaismuuttujan arvoja, saadaan tulokseksi normaalijakauma riippumatta alkuperäisen jakauman muodosta.
Normaalijakaumaa koskevia lauseita
muokkaaJos , niin .
Jos ja ja ovat vakioita, niin .
Jos ovat riippumattomia satunnaismuuttujia ja , niin .
Jos ovat riippumattomia satunnaismuuttujia ja , niin satunnaismuuttujien keskiarvo noudattaa jakaumaa .
Normaalijakauman laskeminen tietokoneella
muokkaaEsimerkiksi Sagella voi laskea normaalijakauman N(0,1) likiarvon seuraavasti:
sage: N(integrate(1/sqrt(2*pi)*exp(-x^2/2),x,-infinity,1)) 0.841344746068543
Vastaavasti numeerisesti voidaan laskea, milloin vaikkapa :
sage: import scipy.stats as st sage: st.norm.ppf(0.95,0,1) 1.6448536269514722
Lähteet
muokkaaAiheesta muualla
muokkaa- Mathworld. Normal Distribution (englanniksi)
- Table of the Standard Normal Distribution (Arkistoitu – Internet Archive) Standardinormaalijakauman kertymäfunktion arvoja (englanniksi)
- The Myth of the Bell Curve. Kritiikkiä normaalijakauman käytöstä yhteiskuntatieteissä. (englanniksi)
- Online laskin Normaalijakauma
- Interaktiivinen Normaalijakauma, Java/Geogebra (Arkistoitu – Internet Archive)
| Diskreettejä jakaumia | |
|---|---|
| Jatkuvia jakaumia | |
| Moniulotteisia jakaumia |


![{\displaystyle {\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sqrt {2\sigma ^{2}}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04670b14acb4ddb796469f3812ead9d9cccec275)














