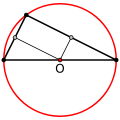
Kolmion ympäri piirretty ympyrä

Kolmion ympäri piirretty ympyrä tarkoittaa geometriassa kolmion kärkien kautta kulkevaa ympyrää. Kolmen pisteen kautta voidaan aina piirtää joko ympyrä tai suora. Jos kolme pistettä ovat kollineaarisia, voidaan niiden kautta piirtää suora. Jos pisteet ovat epäkollineaariset, muodostuu pisteistä kolmio. Koska kolmio on aina konsyklinen, voidaan sen kärkien kautta piirtää ympyrä. Ympyrää kutsutaan myös nimellä ulkoympyrä.

Kolmion ympäri piirretty ympyrä voidaan konstruoiden sivujen keskinormaalien avulla. Keskinormaalit leikkaavat samassa pisteessä, missä on ympyrän keskipiste.

Ympyrän keskipiste voi olla kolmion sisä- tai ulkopuolella. Jos kolmio on teräväkulmainen kolmio, on keskipiste kolmion sisäpuolella. Jos kolmio on suorakulmainen kolmio, on keskipiste kolmion hypotenuusalla. Jos kolmio on tylppäkulmainen kolmio, on keskipiste kolmion ulkopuolella.

• 
  Teräväkulmaisella kolmiolla keskipiste on kolmion sisällä
• 
  Suorakulmaisella kolmiolla keskipiste on hypotenuusalla
• 
  Tylppäkulmaisella kolmiolla keskipiste on kolmion ulkopuolella

Yleinen kolmio

Koordinaateilla

Jos kolmion kärkien koordinaatit merkitään $\scriptstyle P_{1}(x_{1},y_{1}),$ $\scriptstyle P_{2}(x_{2},y_{2})$ ja $\scriptstyle P_{3}(x_{3},y_{3})$, voidaan ympyrän yhtälö kirjoittaa determinantilla

${\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0,$

joka on evaluoituna

$a(x^{2}+y^{2})+b_{x}x+b_{y}y+c=0,$

missä

$a\equiv {\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}},$

x:n kerroin $b_{x}$ saadaan matriisista

$D={\begin{bmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\\\end{bmatrix}}$

jättämällä $x_{i}$ termejä sisältävä sarake pois (vastaavasti $b_{y}$:n suhteen) determinantista

$b_{x}=-{\begin{vmatrix}x_{1}^{2}+y_{1}^{2}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&y_{3}&1\\\end{vmatrix}}$

ja

$b_{y}={\begin{vmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&1\\\end{vmatrix}},$

ja vakiotermi c

$c\equiv -{\begin{vmatrix}x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}\\\end{vmatrix}}.$

Ympyrän yhtälö voidaan esittää keskipistemuodossa

$(x-x_{0})^{2}+(y-y_{0})^{2}=r^{2},$

missä keskipisteen koordinaatit ovat

$x_{0}=-{\frac {b_{x}}{2a}}$

ja

$y_{0}=-{\frac {b_{y}}{2a}}$

sekä säde

$r={\frac {\sqrt {b_{x}^{2}+b_{y}^{2}-4ac}}{2|a|}}.$

Sivujen pituuksilla

Jos kolmion sivujen pituudet merkitään a, b ja c, on säde

$R={\frac {abc}{\sqrt {(a+b+c)(b+c-a)(c+a-b)(a+b-c)}}}.$

Sivun ja kulman avulla

Jos kolmiosta tunnetaan sivu ja sen vastainen kulma, saadaan Sinilauseesta

$R={\frac {a}{2\sin \alpha }}={\frac {b}{2\sin \beta }}={\frac {c}{2\sin \gamma }}.$

Erityinen kolmio

Tasakylkisellä ja -sivuisella kolmiolla

Tasasivuisen kolmion, jonka sivun pituus on a, ympäröivän ympyrän säde R on

$R={\frac {a}{\sqrt {3}}}.$

Tasakylkisellä kolmiolla, jossa kylkien pituudet ovat a ja kannan pituus b säde on

$R={\frac {a^{2}}{\sqrt {4a^{2}-b^{2}}}}.$

Suorakulmaisella kolmiolla

Ympyrän säde on puolet hypotenuusan c eli kolmion pisimmän sivun pituudesta

$R={\tfrac {1}{2}}c$

ja keskipisteen paikka on hypotenuusan keskipisteessä (Thaleen lause).

Lähteet

• Väisälä Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
• Kurittu Lassi: Geometria (pdf) (luentomoniste) 2006. Jyväskylän: Jyväskylän Yliopisto.
• Harju, Tero: Geometrian lyhyt kurssi (pdf) (luentomoniste) users.utu.fi. 2012. Turun yliopisto. Viitattu 14.12.2012.

Aiheesta muualla

• Circumcircle of a triangle