Normi (matematiikka)

Matematiikassa normi on itseisarvon käsitteen yleistys, "vektorin pituus". Normi on kuvaus, joka asettaa jokaista lineaariavaruuden alkiota vastaamaan reaaliluvun. Tietyssä mielessä normi määrittää vektorin etäisyyden origosta, jota voi intuitiivisesti hahmottaa vektorin pituutena. Esimerkiksi $\scriptstyle \mathbb {R} ^{2}$-tason vektoreille $(x,y)$ käytetään yleensä Pythagoraan lausetta vastaavaa normia $\|(x,y)\|=\scriptstyle {\sqrt {x^{2}+y^{2}}}$.

Yksikköympyröitä eri normeissa.

Määritelmä

Olkoon $X$ lineaariavaruus kerroinkuntana $\mathbb {K}$. Tällöin kuvaus $p:X\rightarrow \mathbb {R}$ on normi (joukossa X), jos se toteuttaa seuraavat ehdot

1. $p(x)\geq 0$ kaikilla $x\in X$,
2. $p(x)=0$ jos ja vain jos $x={\bar {0}}$ (=nollavektori),
3. Kuvaus p on skaalautuva: $p(kx)=|k|p(x)$ kaikilla $x\in X$ ja $k\in \mathbb {K}$,
4. Kuvaus p toteuttaa ns. kolmioepäyhtälön: $p(x+y)\leq p(x)+p(y)$ kaikilla $x,y\in X$.

Normia p merkitään usein kirjallisuudessa symbolilla $||\cdot ||$ ja sen arvoa $p(x)=||x||$. Jos lineaariavaruuteen X on määrätty normi p, niin paria (X,p) kutsutaan normiavaruudeksi.

Seminormi on kuvaus, joka toteuttaa normin kaikki muut ehdot paitsi ehdon 2.

Ominaisuuksia

Jokainen normiavaruus on luonnollisella tavalla metrinen avaruus. Nimittäin jos $(X,||\cdot ||)$ on normiavaruus, niin kuvaus $d:X\times X\rightarrow \mathbb {R}$, $d(x,y)=||x-y||$ on metriikka. Kutsumme tämmöisen ns. normimetriikan virittämää topologiaa tavalliseksi topologiaksi.

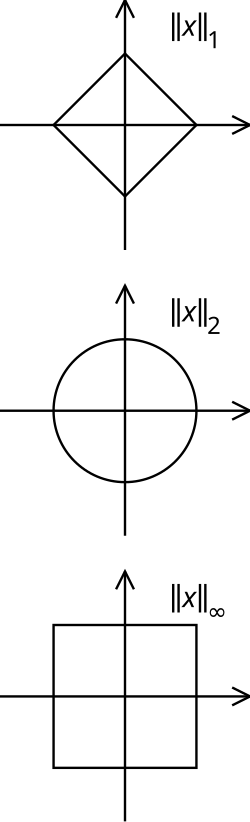
Metrisenä avaruutena normiavaruuteen voidaan myös määritellä ns. yksikköympyrä. Normiavaruuden $(X,||\cdot ||)$ x-keskinen, r-säteinen yksikköympyrä on joukko $\{y\in X:||x-y||=r\}$. Vaihtamalla siis normia avaruudessa X saamme aina mahdollisesti erilaisia yksikköympyröitä. Oheisissa kuvissa on joukon $\mathbb {R} ^{2}$ erilaisten normien määräämiä yksikköympyröitä.

Esimerkkejä normeista

• Euklidinen normi joukossa $\mathbb {R} ^{n}$: ${||x||}_{2}={\sqrt {x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}}$
• $L^{p}$- ja $\ell ^{p}$-normit:

- Jonoavaruuden $\mathbb {R} ^{\mathbb {N} }$ osajoukon $\ell ^{p}$-äärellisten jonojen joukon ns. $\ell ^{p}$-normi ${||\cdot ||}_{p}$ saadaan kaavasta

${||x||}_{p}={\sqrt[{p}]{\sum _{i=1}^{\infty }{|x_{i}|}^{p}}}$

- Funktioavaruuden $L^{p}$ ns. $L^{p}$-normi ${||\cdot ||}_{p}$ saadaan kaavasta

${||f||}_{p}={\sqrt[{p}]{\int |f|^{p}}}$

• Maksiminormit rajoitettujen jonojen avaruudessa $\ell ^{\infty }$ ja oleellisesti rajoitettujen funktioiden avaruudessa $L^{\infty }$: ${||x||}_{\infty }=\max\{x_{i}:i\in \mathbb {N} \}$ ja

${||f||}_{\infty }={\mbox{ess sup}}|f|$

Kirjallisuutta

• Jalava, Väinö: Moderni analyysi I. (15) Tampere: TTKK, 1976. ISBN 951-720-223-7