Pallotrigonometria

Pallotrigonometria tarkoittaa kolmiomittausta pallon pintaa pitkin. Koska pallopinta eroaa kaarevuutensa vuoksi tasosta, myös pallotrigonometrialla on eroja koulusta tuttuun tason trigonometriaan verrattuna. ^[1] Pallotrigonometrialla on perinteisesti ollut erityisen suuri merkitys tähtitieteessä sekä navigoinnissa.

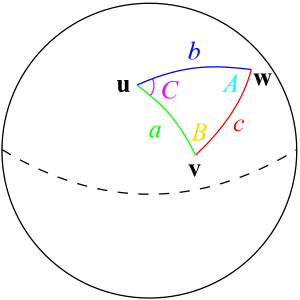
Eräs pallokolmio. Kulmat a, b ja c vastaavat kolmion sivuja ja C on sivun c vastainen kärkikulma. Vastaavalla tavalla kärjessä v on kulma B ja kärjessä w on kulma A.

Pallokolmio muokkaa

Pallotrigonometrian perusobjekti on pallokolmio. Pallokolmio muodostuu kolmen pallon keskipisteen kautta kulkevan tason ja pallon pinnan leikkauksena syntyvistä pallon isoympyrän kaarista. Pallokolmion kulmat ovat näiden tasojen väliset kulmat eli diedrikulmat. Koska isoympyrän kaarien suuruus ilmaistaan niitä vastaavien keskuskulmien suuruutena, pallokolmion sivut ja kulmat ilmoitetaan molemmat kulmamitoin. Pallotrigonometrian sovelluksissa käytetään lähes yksinomaan kulman mittayksikkönä astetta, mutta joissakin teoreettisissa tarkasteluissa on hyödyllisempää käyttää radiaaniyksikköä.

Olkoon $O$ pallon keskipiste. Pallokolmion $ABC$ napakolmio on $A'B'C'$ , missä $OA'$ on tason $OBC$ normaali ja $A'$ on se normaalin ja pallon leikkauspiste, josta tarkasteltuna kaari $BC$ kuljetaan positiiviseen kiertosuuntaan ja $B'$ , $C'$ määritellään analogisesti. Napakolmion sivuille $a',\,b'\,c'$ pätee $a'=180^{\circ }-A$ , $b'=180^{\circ }-B$ ja $c'=180^{\circ }-C$ . Osoittautuu, että kolmion $A'B'C'$ napakolmio on $ABC$ . Siis $a=180^{\circ }-A'$ , $b=180^{\circ }-B'$ ja $c=180^{\circ }-C'$ .

Pallotrigonometrian kaavoja muokkaa

Pallokolmioiden tuntemattomien osien laskeminen tunnettujen osien avulla perustuu pallotrigonometrian sini- ja kosinilauseisiin. Jos pallokolmion kulmat ovat $A$ , $B$ ja $C$ (pallokolmion kulmia ja sen kärkiä on tapana merkitä samalla symbolilla) ja niiden vastaiset sivut $a$ , $b$ ja $c$ , niin pallotrigonometrian sinilauseen ilmaisevat yhtälöt

{\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}

.

Pallotrigonometrian (ensimmäinen) kosinilause puolestaan sisältyy yhtälöön

\cos a=\cos b\,\cos c+\sin b\,\sin c\,\cos A

(ja siitä symbolien kiertovaihteluilla muodostettuihin yhtälöihin).

Pallotrigonometrian toinen kosinilause puolestaan sisältyy yhtälöön

\cos A=-\cos B\,\cos C+\sin B\,\sin C\,\cos a

(ja siitä symbolien kiertovaihteluilla muodostettuihin yhtälöihin).

Pallotrigonometrian ensimmäisen kosinilauseen todistamiseksi oletetaan pallon säteeksi 1. Merkitään pallokolmion kärkipisteitä samoilla kirjaimilla kuin sen kulmia ja pallon keskipistettä $O$ :lla. Tason $OAB$ normaalivektori on ${\overrightarrow {OA}}\times {\overrightarrow {OB}}$ ja tason $OAC$ normaalivektori on ${\overrightarrow {OA}}\times {\overrightarrow {OC}}$ . Kerrottavien vektorien pituus on 1, joten ristitulojen pituudet ovat $\sin c$ ja $\sin b$ . Lisäksi ${\overrightarrow {OA}}\cdot {\overrightarrow {OB}}=\cos c$ , ${\overrightarrow {OB}}\cdot {\overrightarrow {OC}}=\cos a$ ja ${\overrightarrow {OC}}\cdot {\overrightarrow {OA}}=\cos a$ . Normaalivektorien pistetulon avulla voidaan ilmaista tasojen $OAB$ ja $OAC$ välisen kulman kosini eli $\cos A$ : $\sin b\sin c\cos A=({\overrightarrow {OA}}\times {\overrightarrow {OB}})\cdot ({\overrightarrow {OA}}\times {\overrightarrow {OC}})={\overrightarrow {OA}}\cdot ({\overrightarrow {OB}}\times ({\overrightarrow {OA}}\times {\overrightarrow {OC}}))={\overrightarrow {OA}}\cdot (({\overrightarrow {OB}}\cdot {\overrightarrow {OC}}){\overrightarrow {OA}}-({\overrightarrow {OB}}\cdot {\overrightarrow {OA}}){\overrightarrow {OC}})=\cos a-\cos b\cos c.$ Edellä käytettiin tietoa kertomisjärjestyksen vaihtamismahdollisuudesta skalaarikolmitulossa ja vektorikolmitulon laskukaavaa.

Pallotrigonometrian sinilause voidaan johtaa kosinilauseesta trigonometrian peruskaavojen avulla ja toinen kosinilause on ensimmäinen kosinilause sovellettuna $ABC$ :n napakolmioon $A'B'C'$ .

Pallokolmion palloylijäämä muokkaa

Tasogeometrian kolmion kulmasummalause ei päde pallokolmioille. Pallokolmion kulmien summa on aina suurempi kuin $180^{\circ }$ . Tämän todistamiseksi tarkastellaan ensin pallokolmiota $ABC''$ , missä $C''$ on pisteen $C$ antipodipiste eli $C$ :stä piirretyn pallon halkaisijan toinen päätepiste. Tämän kolmion sivut ovat $180^{\circ }-a,\,180^{\circ }-b,\,c$ . Koska isoympyrän kaari $c=AB$ on pallon geodeettinen viiva eli lyhin tie pisteestä $A$ pisteeseen $B$ , on $c<(180^{\circ }-a)+(180^{\circ }-b)$ eli $a+b+c<360^{\circ }$ . Pallokolmion sivujen pituus on siis enintään $360^{\circ }$ . Kun tämä relaatio sovitetaan napakolmioon ja otetaan huomioon napakolmion sivujen ja alkuperäisen kolmion kulmien välinen yhteys, saadaan $360^{\circ }>a'+b'+c'=(180^{\circ }-A)+(180^{\circ }-B)+(180^{\circ }-C)$ eli $A+B+C>180^{\circ }$ . Pallokolmion ja tasokolmion kulmien summien erotusta $E$ kutsutaan palloylijäämäksi tai pallokolmioylijäämäksi (engl. spherical excess). Jos pallokolmion kulmien $A$ , $B$ ja $C$ suuruudet on ilmoitettu radiaaneissa, palloylijäämä on

E=(A+B+C)-\pi \,

.

Pallokolmion pinta-ala $S$ on suorassa yhteydessä sen palloylijäämään. Jos kulmayksikkönä käytetään radiaania, on

S=Er^{2}\,

,

missä $r$ on pallon säde. On nimittäin helppo nähdä, että pallokaksikulmiot, joiden kärjet ovat pallokolmion kärkiä ja sivut pallokolmion jatkeita, peittävät yhteensä puolipallon pinnan ja sen lisäksi kahdesti pallokolmion $ABC$ . Koska pallokaksikolmioiden alat ovat (jos kulmat ilmaistaan radiaaneina) $A/(2\pi )\,$ , $B/(2\pi )\,$ ja $C/(2\pi )\,$ koko pallon pallon pinta-alasta eli $2Ar^{2}\,$ , $2Br^{2}\,$ ja $2Cr^{2}\,$ , saadaan yhtälö $2(A+B+C)r^{2}=2\pi r^{2}+2S\,$ , mistä $S=Er^{2}\,$ .

Täten palloylijäämä ilmoittaa (steradiaaneissa) sen avaruuskulman, jossa pallokolmio näkyy pallon keskipisteestä katsottuna.

Isoympyräetäisyys muokkaa

Pallotrigonometrian ensimmäisen kosinilauseen avulla voidaan määrittää kahden maapallon pinnan pisteen $B$ ja $C$ lyhin etäisyys, kun pisteiden maantieteelliset koordinaatit tunnetaan. Muodostetaan pallokolmio, jonka yksi kärki ( $A$ ) on pohjoisnapa ja toiset kärjet $B$ ja $C$ . Tällöin $b$ (tai $c$ ) on joko $90^{\circ }-$ pisteen leveyskoordinaatti (jos piste on pohjoisella pallonpuoliskolla) tai $90^{\circ }+$ pisteen leveyskoordinaatti (jos piste on eteläisellä pallonpuoliskolla). Kulma $A$ on joko pisteiden $B$ ja $C$ pituuskoordinaattien erotus (jos pisteet ovat molemmat itäisellä tai molemmat läntisellä pallonpuoliskolla) tai pienempi luvuista pituuskoordinaattien summa ja $180^{\circ }-$ pituuskoordinaattien summa (jos toinen piste on läntisellä ja toinen itäisellä pallonpuoliskolla). Ensimmäinen kosinilause kertoo pisteitä $B$ ja $C$ yhdistävän ispoympyräkaaren kosinin; kun tästä määritetään kulma $a$ ja otetaan huomioon maapallon ympärysmitta noin 40000 km, saadaan isoympyräkaaren $BC$ pituus ${\frac {a}{360^{\circ }}}\cdot 40000$ km.