Monotoninen funktio
Monotoninen funktio on matematiikassa funktio, jonka arvot pelkästään kasvavat tai vähenevät määrittelyjoukossaan. [1]
Määritelmästä voidaan erottaa kaksi erillistä tapausta:
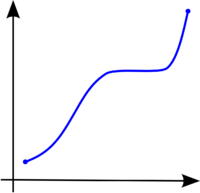
- Funktio on monotonisesti kasvava, jos muuttujan arvojen kasvaessa myös funktion arvot kasvavat, eli jos siitä seuraa . [1]
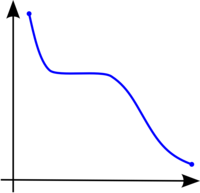
- Funktio on monotonisesti vähenevä, jos muuttujan arvojen kasvaessa funktion arvot sen sijaan vähenevät, eli jos siitä seuraa . [1]
Kummatkin tapaukset sisältyvät yleiseen määritelmään monotonisesta funktiosta. [1]
Funktio on aidosti monotoninen, jos se on aidosti kasvava tai aidosti vähenevä:
- Funktio on aidosti kasvava, kun jos niin silloin . [1]
- Funktio on aidosti vähenevä, kun jos niin silloin . [1]
Reaaliluvuilla aidosti monotoninen funktio on samalla bijektio määrittelyjoukolta arvojoukolleen. Se ei kuitenkaan välttämättä ole :n bijektio :lle, sillä esimerkiksi eksponenttifunktio ex on aidosti kasvava, mutta se ei saa millään reaalilukuarvolla negatiivisia arvoja.
Monotonisuuden tutkiminen
muokkaaMääritelmä antaa tyydyttävän perusteen selvittää tavallisen yksiarvoisen funktion monotonisuutta. Käytännössä on kuitenkin mahdotonta todistaa yksittäinen funktio monotoniseksi, koska silloin täytyisi osoittaa kaikille lukupareille ja määritelmä todeksi. Käytännössä määritelmää käytetään osoittamaan jokin funktion monotonisuus epätodeksi.
Käytännössä monotonisuus osoitetaan erotusosamäärän
avulla. Jos eli kaikille lukupareille ja , niin määritelmän mukaan aidosti kasvavalle funktiolle pätee silloin aina eli myös . Muodostettu erotuksien osamäärä tulee positiiviseksi, jos molemmat erotukset ovat saman merkkiset. Funktio on tällöin aidosti kasvava. Jos erotuksien merkit ovat erit, tulee osamäärä negatiiviseksi ja funktio on aidosti vähenevä.
Erotusosamäärän testaaminen eri lukupareilla ei ole käytännöllistä, vaan erotusosamäärän lauseke muutetaan funktion derivaattafunktioksi toisen pisteen suhteen
tai vaihtamalla merkintöjä niin, että esitetään derivaattafunktion lauseke kohdassa x
- .
Derivaattafunktion ominaisuuksia tutkimalla voidaan päätellä monotonisuuden laatua ja vaihtumista. Monotonisuuden voi jaotella derivaattafunktion ominaisuuksien mukaan koko tarkasteluvälillä seuraavasti:
- Jos , on funktio aidosti kasvava.
- Jos , on funktio kasvava.
- Jos , on funktio aidosti vähenevä.
- Jos , on funktio vähenevä.
Aito monotonisuus täsmällisesti määriteltynä: derivoituva funktio on aidosti kasvava, kun ja jos ei ole olemassa väliä, jolla . Esimerkiksi funktio on aidosti kasvava, vaikka sen derivaattafunktio ei ole kaikkialla suurempi kuin 0. Kyseisen funktion derivaatta onkin 0 vain yksittäisessä pisteessä: . Ja , kun . Funktion derivaatta voi siis olla yksittäisissä pisteissä 0 ilman, että menettää aidon monotonisuutensa.
Vastaavasti (derivoituva) funktio on aidosti vähenevä, kun ja jos ei ole olemassa väliä, jolla .
Esimerkkejä monotonisista funktioista
muokkaaAidosti kasvavia alkeisfunktioita koko laajimmassa määrittelyjoukossaan ovat muun muassa muut eksponenttifunktiot (kantaluku > 1), logaritmifunktio, parittomat potenssifunktiot, juurifunktiot, tangenttifunktio ja arcustangenttifunktio.
Aidosti väheneviä alkeisfunktioita ovat muun muassa muut laskevat lineaariset funktiot ja eksponenttifunktiot (0 < kantaluku < 1).
Eksponenttifunktio on aidosti kasvava funktio koko reaalilukualueessa. Negatiivisilla x:n arvoilla funktion kasvuvauhti on pieni, mutta positiivisilla arvoilla se kasvaa nopeasti. Eksponenttifunktion derivaattafunktio on myös eksponenttifunktio , joka on positiivinen eli kaikilla x:n arvoilla. Tämä täyttää monotonisuusehdon.
Toisen asteen potenssifunktio ei ole monotoninen funktio. Kuvaajasta nähdään, että funktion arvot vähenevät negatiivisilla x:n arvoilla ja kasvavat positiivisilla x:n arvoilla. Jos määrittelyjoukkosta poistettaisiin kaikki negatiiviset luvut, olisi kuvaus
aidosti kasvava funktio. Negatiivisilla arvoilla kuvaus
olisi aidosti vähenevä funktio.
Lähteet
muokkaa- Tampereen Teknillinen Korkeakoulu: Funktion ominaisuuksia (Arkistoitu – Internet Archive)
- Jyväskylän yliopisto: Funktion monotonisuus
- Helsingin yliopisto: Matematiikan tukikurssi, #8
- Wolframs Mathworld: Monotonic functions
- Connexions: Monotonic functions
- Swarthmore: Monotonic functions (Arkistoitu – Internet Archive)
- Math eCources: Monotonic functions (Arkistoitu – Internet Archive)
Viitteet
muokkaaKirjallisuutta
muokkaa- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf). Viitattu 8.7.2019.