Kiihtyvyys
Kiihtyvyys (tunnus ) on fysikaalinen vektorisuure, joka kuvaa kappaleen nopeuden muutosta ajan funktiona. Vektorisuureena sillä on suunta ja suuruus, mutta lineaarista liikettä voidaan tarkastella skalaarisen kiihtyvyyden avulla. Kiihtyvyyden yksikkö on SI-järjestelmässä m/s². Putoamiskiihtyvyydelle maan pinnan läheisyydessä käytetään tunnusta .[1]
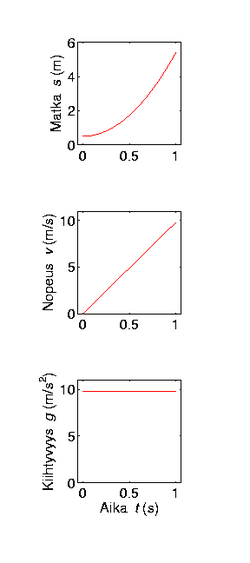
Kappaleen kiihtyvyys määritellään fysiikassa nopeuden ensimmäisenä ja toisaalta siirtymän (paikan muutos) toisena derivaattana ajan suhteen:
missä
- = kappaleen kiihtyvyysvektori
- = kappaleen nopeusvektori
- = kappaleen siirtymävektori
- t = aika.
Kappaleen keskikiihtyvyys on sen nopeuden muutos jaettuna aikavälin pituudella:
Tästä huomataan, että mitä pienemmällä aikavälillä keskikiihtyvyyttä tarkastellaan, sitä tarkemmin se kuvaa todellista hetkellistä kiihtyvyyttä.
Tasainen ja tasaisesti kiihtyvä liike
muokkaaTasaisessa liikkeessä kiihtyvyys on nolla. Tasaisesti kiihtyvässä liikeessä kiihtyvyys on vakio, ja se voidaan yksinkertaisesti laskea keskikiihtyvyyden kaavalla
Jos tasaisesti kiihtyvässä liikkeessä olevan kappaleen nopeus sovitulla hetkellä t0 on v0 ja kiihtyvyys samaan suuntaan on a, niin hetkellä t sen nopeus on , ja tässä ajassa se on kulkenut matkan
.[3]
Tietyllä aikavälillä kappaleen keskikiihtyvyys on sen nopeuksien erotus aikavälin lopussa ja alussa jaettuna aikavälin pituudella:
Tasaisesti kiihtyvän liikkeen kiihtyvyys on siis koko ajan yhtä suuri kuin sen keskikiihtyvyys. Muussa tapauksessa kappaleen hetkellinen kiihtyvyys saadaan sen keskikiihtyvyyden raja-arvona, kun tarkasteltava aikaväli on mahdollisimman lyhyt.[3]
Yksiulotteisessa liikkeessä suunta voidaan unohtaa ja kiihtyvyys on suoraan nopeuden kuvaajan tangentti. Tasaisesti kiihtyvässä liikkeessä nopeus ajan funktiona piirrettynä antaa suoran, jonka kulmakertoimesta kiihtyvyys voidaan laskea. Kuvaaja voi olla kuitenkin monimutkaisempi, jos esimerkiksi piirretään auton nopeus ruuhkassa ajan funktiona. Tällöin kiihtyvyys ei ole vakio.
Kiihtyvyys ympyräliikkeessä
muokkaaKiihtyvyys ympyräliikkeessä voidaan jakaa kahteen komponenttiin, kappaleen tangentin suuntaiseen tangenttikiihtyvyyteen, sekä sitä vastaan kohtisuoraan (säteen suuntaiseen) normaalikiihtyvyyteen. Molempia suureita tarkasteltaessa tärkeiksi työkaluiksi tulee kulma , kulmanopeus ( ) ja kulmakiihtyvyys ( ). Kulmakiihtyvyys voidaan määrittää vastaavasti kuin kiihtyvyys kulmanopeuden ensimmäisenä ja toisaalta kulman muutoksen toisena derivaattana ajan suhteen
Tangenttikiihtyvyys ja normaalikiihtyvyys voidaan ilmoittaa kulmanopeuden , kulmakiihtyvyyden ja ympyrän säteen avulla:
Kiihtyvyys voi vaikuttaa sekä kappaleen vauhdin suuruuteen, että suunnan muutokseen. Jos tangentiaalikiihtyvyys on ympyräradalla kulkevan kappaleen nopeuden suuntainen, kappaleen vauhti kasvaa; jos se taas on vastakkaissuuntainen, liike hidastuu. Normaalikiihtyvyys taas vaikuttaa ympyräradan jyrkkyyteen eli siihen kuinka nopeasti kappaleen suunta muuttuu. Mitä suurempi normaalikiihtyvyys on, sitä pienemmällä ympyräradalla kappale liikkuu. Jos normaalikiihtyvyys putoaa nollaan, kappale poistuu ympyräradalta ja jatkaa tasaista suoraviivaista liikettä, ellei siihen vaikuta muita kiihtyvyyksiä.
Kiihtyvyys törmäyksissä
muokkaaTörmäyksessä tapahtuvaa äkkinäistä nopeuden muutosta mitataan G-yksiköissä. 1 G on putoamiskiihtyvyys eli maan vetovoiman aiheuttama kiihtyvyys maan pinnalla, joka on noin 9,81 m/s2. Esimerkiksi kirpun kokema hidastuvuus voi olla jopa 50 G:n suuruinen sen osuessa puunrunkoon siihen hypättyään. Tämä kiihtyvyys on SI-järjestelmän yksiköinä noin 50 · 9,81 m/s2 = 490 m/s2.
Kiihtyvyys ja dynamiikan peruslaki
muokkaaDynamiikan II. peruslain mukaan kappaleeseen kohdistuva kokonaisvoima aiheuttaa sille kiihtyvyyden.
Katso myös
muokkaaLähteet
muokkaa- ↑ Suomen standardisoimisliitto SFS: SI opas, s. 14. SFS Standardisointi, 2002.
- ↑ a b Hugh D. Young & Roger A Freedman: Fyysikko, s. 94. Mark Zemansky & Francis Sears, 2012.
- ↑ a b c Kaarle ja Riitta Kurki-Suonio: Vuorovaikuttavat kappaleet – mekaniikan perusteet, s. 20. Limes r.y., 1995. ISBN 9517451679.
Aiheesta muualla
muokkaa- Kuvia tai muita tiedostoja aiheesta Kiihtyvyys Wikimedia Commonsissa







