Kierre

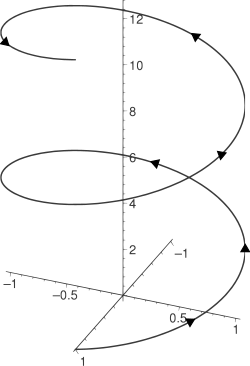
Matematiikassa kierre eli ruuviviiva on avaruudessa tasaisesti kaartuva käyrä, joka etenee akselinsa suuntaisesti.

Kierre (cos t, sin t, t) t:n arvoilla 0 ... 4π; nuolten kärjet osoittavat suunnan, johon mentäessä parametri t kasvaa

Kierre on myös ruuveissa ja muttereissa oleva työstetty muoto.

Ominaisuuksia

Kierre on lieriön geodeettinen viiva. Jos lierön vaippapinta levitetään tasoksi, sillä oleva kierre muuttuu suoraksi.

Kierteelle mihin tahansa pisteeseen sijoitetulla tangentilla on olemassa yksi akseliin osoittava normaali. Näiden normaalien ne osat, jotka ovat kierteen ja akselin välissä, muodostavat ruuvipinnan.

Erityyppisiä kierteitä

Kierre voi olla oikea- tai vasenkätinen. Jos kierteen akselin suuntaan katsottaessa käyrä kiertää myötäpäivään etääntyessään katsojasta, on kyseessä oikeakätinen, muussa tapauksessa vasenkätinen kierre. Tämä kätisyys on kierteen oma ominaisuus eikä riipu havaitsijan sijainnista: oikeakätistä kierrettä ei voi yhdensuuntaissiirrolla tai rotaatiolla muuttaa vasenkätiseksi tai päinvastoin.

Ruuvit tehdään lähes aina niin, että niiden kierteet ovat oikeakätisiä. Elollisessa luonnossa esiintyy oikeakätinen kierre DNA-molekyylin A- ja B-muodoissa, kun taas Z-DNA:ssa on vasenkätinen kierre.

Matemaattinen kuvaus

Sinusoidisten x- ja y-komponenttien muodostama kierre

Oikeakätisen kierteen yhtälöt, kun kierteen akselina on z-akseli, voidaan esittää karteesisilla koordinaateilla parametrimuodossa seuraavasti:

$x(t)=a\cos(t),\,$

$y(t)=a\sin(t),\,$

$z(t)=bt.\,$

Tässä vakio a on sen lieriön säde, jonka pinnalla kierre on. Kun parametri t kasvaa, piste (x(t),y(t),z(t)) kulkee oikeakätisen kierteen muotoista rataa, missä täysi kierros akselin ympäri tulee tehdyksi aina, kun t kasvaa määrän 2π/b. Tällöin on edetty z-akselin suunnassa matkan 2πb verran.

Sylinterikoordinaateilla (r, θ, h) sama kierre voidaan esittää parametrimuodossa seuraavasti:

$r(t)=a,\,$

$\theta (t)=t,\,$

$h(t)=bt.\,$

Katso myös

• Spiraali
• Alfa-kierre
• DNA

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Kierre Wikimedia Commonsissa