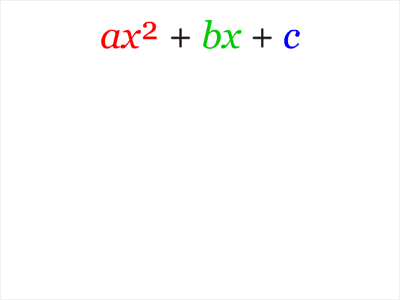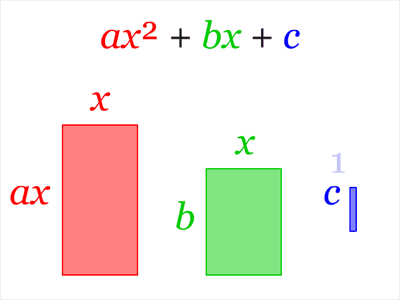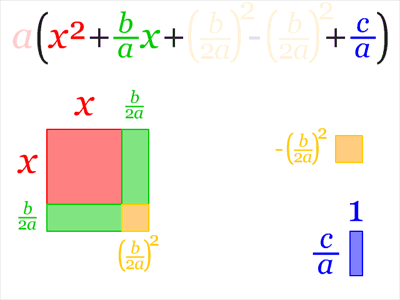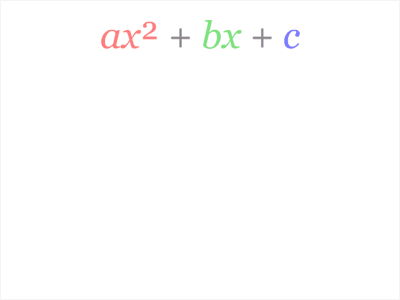Neliöksi täydentäminen on algebrallinen menetelmä toisen asteen yhtälön ratkaisemiseksi. Neliöksi täydentämistä voidaan soveltaa myös integraaleja laskettaessa .
Neliöksi täydentäminen esitettynä neliölauseke tulkittuna pinta-alaksi. Menetelmän tavoitteena on päästä muodosta (1)
a
x
2
+
b
x
+
c
{\displaystyle ax^{2}+bx+c}
(
a
′
x
+
b
′
)
2
+
c
′
{\displaystyle (a'x+b')^{2}+c'}
Neliöksi täydennyksessä otetaan ensimmäisen asteen termin kertoimen puolikkaan neliö ,
ja lisätään ja vähennetään se. Tälle toimenpiteelle on voimassa ehto, että toisen asteen termin kerroin on 1.
Halutaan tietää mitkä muuttujan x arvot toteuttavat yhtälön:
4
x
2
+
4
x
=
0
{\displaystyle 4x^{2}+4x=0}
Täydennetään neliöksi lisäämällä ja vähentämällä 1.
(
4
x
2
+
4
x
+
1
)
−
1
=
0
(
2
x
+
1
)
2
−
1
=
0
{\displaystyle {\begin{aligned}\left(4x^{2}+4x+1\right)-1&=0\\(2x+1)^{2}-1&=0\end{aligned}}}
Välivaiheittain:
(1) Otetaan termin
x
2
{\displaystyle x^{2}}
4
(
x
2
+
x
)
=
0
{\displaystyle 4\left(x^{2}+x\right)=0}
(2) Täydennetään neliöön: ts. otetaan ensimmäisen asteen kertoimen, eli
1
∗
x
{\displaystyle 1*x}
(
1
2
)
2
=
1
4
{\displaystyle \left({\frac {1}{2}}\right)^{2}={\frac {1}{4}}}
4
[
(
x
2
+
x
+
1
4
)
−
1
4
]
=
0
{\displaystyle 4\left[\left(x^{2}+x+{\frac {1}{4}}\right)-{\frac {1}{4}}\right]=0}
(3) Poistetaan hakasulkeet, jolloin
4
(
x
2
+
x
+
1
4
)
−
1
=
0
4
(
x
+
1
2
)
2
−
1
=
0
(
2
x
+
1
)
2
−
1
=
0
{\displaystyle {\begin{aligned}4\left(x^{2}+x+{\frac {1}{4}}\right)-1&=0\\4\left(x+{\frac {1}{2}}\right)^{2}-1&=0\\(2x+1)^{2}-1&=0\end{aligned}}}
Nyt yhtälö ratkeaa helposti
(
2
x
+
1
)
2
=
1
2
x
+
1
=
±
1
2
x
=
−
1
±
1
x
=
−
1
2
±
1
2
.
{\displaystyle {\begin{aligned}(2x+1)^{2}&=1\\2x+1&=\pm 1\\2x&=-1\pm 1\\x&=-{\frac {1}{2}}\pm {\frac {1}{2}}{\text{.}}\end{aligned}}}
Siis x on joko 0 tai -1.
Toisen asteen polynomifunktion neliöksi täydentäminen tehdään yleisesti seuraavasti:
f
(
x
)
=
a
x
2
+
b
x
+
c
=
a
(
x
+
b
2
a
)
2
+
c
−
b
2
4
a
{\displaystyle f(x)=ax^{2}+bx+c=a\left(x+{b \over {2a}}\right)^{2}+c-{b^{2} \over {4a}}}
Menetelmästä on se etu, että funktion käännepiste voidaan määrittää turvautumatta derivointiin. Käännepiste saadaan yhtälöstä
x
+
b
2
a
=
0
{\displaystyle x+{b \over {2a}}=0}
f
(
−
b
2
a
)
=
c
−
b
2
4
a
{\displaystyle f\left(-{b \over {2a}}\right)=c-{b^{2} \over {4a}}}
Funktion neliöksi täydentäminen tarkoittaa myös koordinaatiston origon . Jos funktio on täydennetyssä muodossaan
y
=
a
(
x
+
b
2
a
)
2
+
c
−
b
2
4
a
{\displaystyle y=a\left(x+{b \over {2a}}\right)^{2}+c-{b^{2} \over {4a}}}
sille saadaan myös seuraava muoto
y
−
(
c
−
b
2
4
a
)
=
a
(
x
+
b
2
a
)
2
.
{\displaystyle y-\left(c-{b^{2} \over {4a}}\right)=a\left(x+{b \over {2a}}\right)^{2}{\text{.}}}
Merkitään
{
x
′
=
x
+
b
2
a
y
′
=
y
−
(
c
−
b
2
4
a
)
.
{\displaystyle {\begin{cases}x'=x+{b \over {2a}}\\y'=y-\left(c-{b^{2} \over {4a}}\right)\end{cases}}{\text{.}}}
Tällöin alkuperäinen funktio saadaan muotoon
y
′
=
(
x
′
)
2
{\displaystyle y'=(x')^{2}}
ja alkuperäinen origo on pisteessä
(
x
,
y
)
=
(
−
b
2
a
,
c
−
b
2
4
a
)
{\displaystyle (x,y)=\left(-{b \over {2a}},c-{b^{2} \over {4a}}\right)}
(
x
′
,
y
′
)
=
(
0
,
0
)
.
{\displaystyle (x',y')=(0,0).}
Tehtävä: kirjoita hyperbelin
9
x
2
−
y
2
+
36
x
+
2
y
+
26
=
0
{\displaystyle 9x^{2}-y^{2}+36x+2y+26=0}
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
vakiot yhtälön oikealle puolelle ja tuntemattomat vasemmalle. Järjestellään x:t ja y:t.
9
x
2
+
36
x
−
y
2
+
2
y
=
−
26
{\displaystyle 9x^{2}+36x-y^{2}+2y=-26}
(2) Ryhmitellään lausekkeet sellaisiksi, että toisen asteen termien kertoimet ovat sulkeiden sisällä 1. Otetaan x-termien yhteinen kerroin 9 ja y-termien kerroin -1 ulkopuolelle.
9
(
x
2
+
4
x
)
+
(
−
1
)
(
y
2
−
2
y
)
=
−
26
{\displaystyle 9\left(x^{2}+4x\right)+(-1)\left(y^{2}-2y\right)=-26}
(3) Täydennetään neliöksi - lisätään ja vähennetään ensimmäisen asteen termien kertoimien puolikkaiden neliöt.
9
[
(
x
2
+
4
x
+
2
2
)
−
2
2
]
+
(
−
1
)
[
(
y
2
−
2
y
+
(
−
1
)
2
)
−
(
−
1
)
2
]
=
−
26
{\displaystyle 9\left[\left(x^{2}+4x+2^{2}\right)-2^{2}\right]+(-1)\left[\left(y^{2}-2y+(-1)^{2}\right)-(-1)^{2}\right]=-26}
(4) Poistetaan hakasulkeet, ja eliminoidaan puolittain "ylimääräinen" neljäs vakio x:n ja y:n lausekkeesta:
9
(
x
2
+
4
x
+
4
)
−
36
+
(
−
1
)
(
y
2
−
2
y
+
1
)
+
1
=
−
26
|
+
36
|
−
1
{\displaystyle 9\left(x^{2}+4x+4\right)-36+(-1)\left(y^{2}-2y+1\right)+1=-26\;|+36\;|-1}
(5) Jolloin jää:
9
(
x
2
+
4
x
+
4
)
+
(
−
1
)
(
y
2
−
2
y
+
1
)
=
9
9
(
x
+
2
)
2
−
(
y
−
1
)
2
=
9
|
:
9
(
x
+
2
)
2
1
−
(
y
−
1
)
2
3
2
=
1
{\displaystyle {\begin{aligned}9\left(x^{2}+4x+4\right)+(-1)\left(y^{2}-2y+1\right)&=9\\9(x+2)^{2}-(y-1)^{2}&=9\;|:9\\{\frac {(x+2)^{2}}{1}}-{\frac {(y-1)^{2}}{3^{2}}}&=1\end{aligned}}}
![{\displaystyle 4\left[\left(x^{2}+x+{\frac {1}{4}}\right)-{\frac {1}{4}}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c82c7bce504362485c84545b952093e15e124e90)
![{\displaystyle 9\left[\left(x^{2}+4x+2^{2}\right)-2^{2}\right]+(-1)\left[\left(y^{2}-2y+(-1)^{2}\right)-(-1)^{2}\right]=-26}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6304184e2c7861ab199a750c4185d8bcf65af73a)
