Hyperboloidi

Hyperboloidi on matematiikassa hyperbelin vastine kolmiulotteisessa avaruudessa. Hyperboloidin yhtälössä oikea puoli määrittää, onko hyperboloidi yksivaippainen, kaksivaippainen vai asymptoottikartion mallinen. Jos yhtälön oikealla puolella on 1, kyseessä on yksivaippainen hyperboloidi; jos nolla, on hyperboloidi asymptoottikartio; jos -1, on kyseessä kaksivaippainen hyperboloidi. Hyperboloidin yhtälön vasemman puolen plus- ja miinusmerkit vaihtelevat sen mukaan, minkä suuntainen hyperboloidi on. Miinusmerkki on aina sen muuttujan edessä, jonka suuntainen hyperboloidi on. Jos hyperboloidi on x-akselin suuntainen, tulee miinusmerkki x-muuttujan eteen ja muille muuttujille positiivinen etumerkki jne.

Yksivaippainen hyperboloidi

Kaksivaippainen hyperboloidi

Asymptoottikartiohyperboloidi

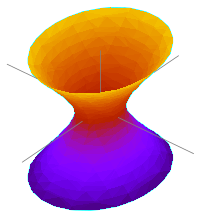
Esimerkkejä hyperboloidin yhtälöstä

Näissä yhtälöissä $a,b,c\in \mathbb {R}$ ja $x,y,z$ ovat muuttujia.

${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1$  (Yksivaippainen z-akselin suuntainen hyberboloidi ),

${x^{2} \over a^{2}}-{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=-1$  (Kaksivaippainen y-akselin suuntainen hyberboloidi )

$-{x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=0$   (Asymptoottikartionmallinen x-akselin suuntainen hyperboloidi)

Jos $a=b$, niin hyperboloidia voidaan kutsua pyörähdyshyperboloidiksi.

Yksivaippainen hyperboloidi rakennettu suorista metallilangoista.

Hyperboloidin tasoleikkaukset

Hyperboloidin tasoleikkaukset ovat ellipsin, paraabelin tai hyperbelin muotoisia riippuen, mistä suunnasta hyperboloidia leikataan.

Hyperboloidin muodostaminen suorista

Kaksivaippaista hyperboloidia ei voi muodostaa suorista sen kahden erillisen osan vuoksi.

Asymptoottikartiohyperboloidin voi muodostaa suorista. Se muodostuu joukosta suoria, jotka kulkevat sen keskipisteen eli kuvassa origon kautta.

Yksivaippaisen hyperboloidin voi myös muodostaa suorista. Näitä suoria kutsutaan hyperboloidin emäsuoriksi ja jokaisen hyperboloidin vaipan pisteen kautta kulkee kaksi eri emäsuorasarjoihin kuuluvaa emäsuoraa. Emäsuorasarjojen yhtälöt saadaan johdettua suoraan itse hyperboloidin yhtälöstä. Helpoiten tämä nähdään kertomalla esimerkiksi ensimmäisen emäsuorasarjan yhtälöt keskenään. Kun kyseessä on esimerkiksi y-akselin suuntainen hyperboloidi, toteuttavat sen emäsuorat seuraavat emäsuorasarjojen yhtälöt:

Emäsuorasarja 1

$\left\{{\begin{matrix}{y \over b}+{z \over c}=\lambda (1-{x \over a})\\{y \over b}-{z \over c}={1 \over \lambda }(1+{x \over a})\end{matrix}}\right.$

Emäsuorasarja 2

$\left\{{\begin{matrix}{y \over b}+{z \over c}=\mu (1+{x \over a})\\{y \over b}-{z \over c}={1 \over \mu }(1+{x \over a})\end{matrix}}\right.$

Näissä emäsuorasarjoissa λ ja μ ovat mielivaltaisia apumuuttujia. Jokaisen λ:n arvolle määrää ensimmäisen emäsuorasarjan yhtälöpari suoran, joka on hyperboloidin pinnalla; samoin jokaiselle μ:n arvolle määrää toisen emäsuorasarjan yhtälöpari suoran, joka on hyperboloidin pinnalla.

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Hyperboloidi Wikimedia Commonsissa