Alkulukufunktio
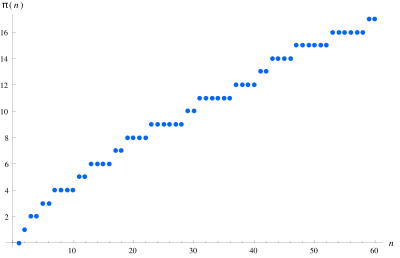
Alkulukufunktio on matematiikan funktio, jolla lasketaan reaalilukua x pienempien tai yhtäsuurten alkulukujen lukumäärää.[1][2][3] Funktion merkintä on (Kaavassa π(x) ei viitata lukuun π.)
Historiaa
muokkaa1700-luvulla löysivät Gauss ja Legendre että
on hyvä approksimaatio alkulukufunktiolle; tarkemmin,
Tämä lauseke tunnetaan alkulukulauseena; se todistettiin 1800-luvun lopulla oikeaksi. Väite voidaan kirjoittaa yhtäpitävästi muodossa
jossa on logaritminen integraalifunktio.
Littlewoodin lause
muokkaaJohn Littlewood todisti 1914 että on olemassa mielivaltaisen suuria lukuja x, joille
ja mielivaltaisen suuria lukuja x, joille
Tästä seuraa että erotuksen π(x) − li(x) merkki vaihtuu äärettömän usein.
Riemannin hypoteesi
muokkaaRiemannin hypoteesi on ekvivalentti seuraavaan kaavaan:
Riemannin hypoteesi siis antaisi alkulukufunktion antamalle arviolle alkulukujen määrästä huomattavasti nykyistä tiukemmat virherajat.
Lähteet
muokkaa- ↑ A table of prime counts pi(x) to 1e16
- ↑ Algorithmic Number Theory, s. volume 1 page 234 section 8.8. MIT Press.
- ↑ Prime Counting Function MathWorld.
