Eulerin suora
Eulerin suora on geometriassa eräiden kolmion merkillisten pisteiden kautta kulkeva suora. Ensimmäiset Eulerin suoralla tunnetut pisteet olivat kolmion painopiste, kolmion ympäri piirretyn ympyrän keskipiste ja kolmion ortokeskus. Nykyään tunnetaan muitakin merkillisiä pisteitä, jotka sijaitsevat Eulerin suoralla. Suora on nimetty Leonhard Eulerin mukaan.[1][2][3]
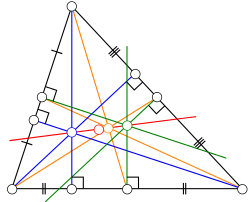

Viitekehys muokkaa
Kolmion merkilliset pisteet tunneettiin jo antiikin kreikassa. Silloin oli huomattu, että kolmion korkeusjanat leikkasivat toisensa aina samassa pisteessä, oli kolmion muoto mikä tahansa. Tätä ominaisuutta pidettiin "merkillisenä". Myös kolmion kulmanpuolittajien ja keskinormaalien tiedettiin tekevän näin.
Vasta klassisella ajalla löydettiin uusia "merkillisiä pisteitä", joista jotkin olivat keskenään samalla suoralla. Eulerin suoran lisäksi tunnetaan esimerkiksi Nagelin suora, Gergonnen suora ja Soddyn suora, joiden nimet ovat lähteistään vapaasti suomennettuja.[4][5][6] Nämä suorat kuuluvat suurempaan suorien joukkoon, josta useimmat ovat nimeämättömiä suoria.[7]
Nykyään merkillisiä pisteitä tunnetaan yli 5 000 ja Eulerin suoralle niistä osuu yli 100. Merkilliset pisteet on luetteloitu muun muassa Kimberlingin merkillisten pisteiden ensyklopediassa tunnuksillä , missä i on pisteen indeksi eli järjestysnumero. Eulerin suoran merkitys on ainakin historiallinen, koska se on ensimmäinen tällainen havaittu suora.[2]
Ominaisuuksia ja erityispiirteitä muokkaa
Eulerin suoralta tunnettiin ensin keskinormaalien leikkauspiste (O = ), korkeusjanojen leikkauspiste eli ortokeskus (H = ) ja mediaanien leikkauspiste eli kolmion painopiste (G = ). Näistä on samalla kolmion ympäri piirretyn ympyrän keskipiste. Neljäs tunnettu piste Eulerin suoralla on yhdeksän pisteen ympyrän (N = ) keskipiste.[2]
Tasasivuisessa kolmiossa pisteet , , ja yhtyvät yhdeksi pisteeksi. Muissa kolmioissa ne ovat aina erillään toisistaan. Pisteiden välimatkojen suhteet säilyvät samoina, vaikka referenssikolmion muoto muuttuisikin. Mikäli mukaan otetaan vielä yksi merkillinen piste, de Longchampsin piste (L = ), suhtautuvat järjestettyjen pisteiden − − − − eli L−O−G−N−H välimatkat suhdeluvuilla 6−2−1−3.[2]
Eulerin suora leikkaa Soddyn suoran de Longchampsin pisteessä ( ) [5], Gergonnen suoran Evansin pisteessä [4] ja Nagelin suoran painopisteessä G eli .[6]
Todistus muokkaa
Olkoon R, S, T kolmion ABC sivujen keskipisteet, H ABC:n ortokeskus, O ABC:n ympäri piirretyn ympyrän keskipiste ja M ABC:n keskijanojen leikkauspiste. Silloin jana RO on kohtisuorassa janan ST kanssa, jana SO kohtisuorassa janan RT kanssa, joten O on RST ortokeskus ja ABC on yhdenmuotoinen ABC:n kanssa. Lisäksi AR ja ST ovat suunnikkaan ATRS lävistäjät, joten ne puolittavat toisensa. Tästä seuraa, että M on myös kolmion RST keskijanojen leikkauspiste. Yhdenmuotoisuudesta seuraa, että molemmissa kolmioissa OMR ja HMA kärjen, ortokeskuksen ja painopisteen muodostamat kolmiot ovat yhdenmuotoiset. Siis kulma OMR = kulma HMA. Tämä tarkoittaa, että O, M ja H ovat samalla suoralla.
Historia muokkaa
Vuonna 1765 Leonhard Euler osoitti, että kaikissa kolmioissa ortokeskus, ympäröivän ympyrän keskipiste ja painopiste ovat kollineaarisia.[8]
Lähteet muokkaa
Viitteet muokkaa
- ↑ Weisstein, Eric W.: Incenter (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b c d Kimberling, Clark: Euler line (html) Tekijän kotisivut. 2013. Evansville: Evansvillen Yliopisto. Viitattu 20.5.2013. (englanniksi)
- ↑ Weisstein, Eric W.: Euler Line (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Weisstein, Eric W.: Gergonne Line (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Weisstein, Eric W.: Soddy Line (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Weisstein, Eric W.: Nagel Line (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Central Line (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Euler, Leonhard (1767). "Solutio facilis problematum quorundam geometricorum difficillimorum". Novi Commentarii academiae scientarum imperialis Petropolitanae 11: 103–123. E325. Reprinted in Opera Omnia, ser. I, vol. XXVI, pp. 139–157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953.