Kiertoheiluri
Kiertoheiluri (torsioheiluri) on heiluri, jossa massakappale on ripustettu yläpäästään kiinnitettyyn kuituun, ja jonka oskillaatio perustuu kuidun kiertymiseen. Massakappaleen oskillaatio (myötäpäivään, vastapäivään, myötäpäivään...) tapahtuu siis kohtisuorasti gravitaatioon nähden, ja gravitaation ainoa merkitys on jännittää kuitua painamalla massakappaletta.[1] Kiertoheilurin palauttava vääntömomentti on suoraan verrannollinen poikkeutuskulmaan ja direktiomomenttiin D,

- .
Kuidun ominaisuuksilla on heilurissa keskeinen merkitys. Kuitu voidaan käsittää pitkänä, ohuena ja kiinteänä tankona. Siihen muodostuu massakappaleen painon vuoksi venymää ja massakappaletta kierrettäessä myös kiertoa. Hooken lain mukaan muodonmuutos on suoraan verrannollinen voimaan eli torsioheilurissa venyminen massakappaleen painoon. Kimmokerroin kuvaa kuormittavan voiman ja venymän suhdetta. Venyminen paitsi pidentää myös ohentaa kuitua. Poissonin luku kuvaa ohenemisen ja venymisen suhdetta. Painon poistamisen pitäisi palauttaa kuitu alkuperäisen muotoiseksi. Laki pätee kuitenkin vain täysin elastisille kappaleille, oikeille kappaleille on olemassa kimmoraja, jonka jälkeen kappale ei enää palaudu alkuperäiseen muotoon painon poistuttua.[1] Kiertoon liittyvä aineelle ominainen liukukerroin kuvaa puolestaan leikkausjännityksen ja poikkeutuskulman suhdetta. Lopulta direktiomomentti riippuu langan ominaisuuksista[1]
- ,
jossa liukukerroin, r kuidun säde ja l kuidun pituus. Erityisen huomioitavaa on kuidun säteen merkitys kiertoheilurin herkkyyteen.[1]

Kiertoheilurin heilahdusaika on samanmuotoinen kuin harmonisen värähtelijän
- ,
jossa I on hitausmomentti.
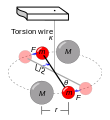
Charles Augustin Coulomb hyödynsi kiertoheiluria muun muassa uraauurtavissa tutkimuksissaan sähkövarausten veto- ja repulsiovoimista 1700-luvun lopulla.[1] Samoihin aikoihin Henry Cavendish puolestaan käytti kiertoheiluria tutkiessaan kappaleiden välisiä gravitaatiovoimia. Kyseinen kiertoheiluriin perustuva laite tunnetaan Cavendishin vaakana. Siinä kiertoheilurin massakappaleena on keskeltä kiinnitetty vaakasuora tanko, jonka päissä on tietyt massat m1. Tangon vieressä, irti tangosta on suuremmat ja paikoilleen kiinnitetyt massat m2. Massojen välinen gravitaatio saa tangon pyörähtämään ja kuidun kiertymään kulman . Kuituun syntyneestä momentista voidaan päätellä kappaleiden vuorovaikutus. Kuidun momentti on suoraan verrannollinen poikkeutuskulmaan , gravitaation tuottama momentti on kääntäen verrannollinen massojen välimatkan neliöön.[1] Coulombin kiertovaa’an periaate oli hyvin lähellä Cavendishin vaakaa; siinä kiertymän tuottivat varatut massakappaleet.
-
Coulombin kiertovaaka (1785)
-
Cavendishin vaaka (1798)
-
Cavendishin vaa'an toiminta