Monty Hallin ongelma

Monty Hallin ongelma on arvoitus, jonka ratkaisu edellyttää todennäköisyyksien arviointikykyä. Ongelma on nimetty Let’s Make a Deal -kisailuohjelman juontajana toimineen Monty Hallin mukaan, ja sen asetelma perustuu löyhästi ohjelman formaattiin.

Pelaaja valitsee oven 1, juontaja avaa oven 3 paljastaen vuohen ja tarjoaa pelaajalle vaihtoa oveen 2.

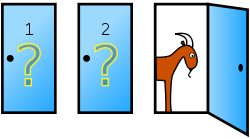
Monty Hallin ongelmassa kilpailijalla on edessään kolme ovea. Yhden oven takana on palkintona auto, kahden muun takana vuohi. Kilpailija, joka ei tiedä minkä oven takana mikin palkinto on, saa valita ovista yhden. Valittuaan oven hän ei vielä avaa sitä. Jäljelle jääneistä kahdesta ovesta avataan toinen, ja sen takana on aina vuohi. Tämän jälkeen kilpailija saa valita, vaihtaako ensin valitsemansa oven toiseen jäljellä olevaan suljettuun oveen, vai pitääkö ensin valitsemansa oven.

Ratkaisu

Mielenkiintoista kilpailijan valinnan kannalta on, että todennäköisyyksien valossa ja useimpien ongelman ratkaisua yrittävien arvion vastaisesti vaihto kannattaa: vaihtamalla ovea voiton todennäköisyys nousee. Ilman vaihtoa voittomahdollisuus on ¹⁄₃, vaihdon jälkeen ²⁄₃.

Eri lopputulemavaihtoehdot, jos oletetaan että pelaaja valitsee oven yksi:

Valittu ovi	Ovi 2	Ovi 3	Tulos vaihtamalla	Tulos pitäytymällä alkuperäisessä
Voitto	Ei voittoa	Ei voittoa	Ei voittoa	Voitto
Ei voittoa	Voitto	Ei voittoa	Voitto	Ei voittoa
Ei voittoa	Ei voittoa	Voitto	Voitto	Ei voittoa

Jos pelaaja vaihtaa valintansa, kahdessa tapauksessa kolmesta hän voittaa.

Todennäköisyyksien muodostumista voi havainnollistaa myös näin: vaihtamalla valintaansa pelaaja häviää vain, jos alun perin valitsi oikean oven, minkä todennäköisyys on ¹⁄₃.

Ratkaisua voi havainnollistaa myös lisäämällä ovia. Jos alun perin ovia on sata, niistä pelaaja valitsee yhden ja lopuista ovista avataan 98 ovea, joiden takana on vuohi. Nyt todennäköisyys sille, että pelaajan valitseman oven takana oli auto, on ¹⁄₁₀₀ ja toisen jäljellä olevan oven voittotodennäköisyys ⁹⁹⁄₁₀₀.

Ratkaisu Bayesin teoreemalla

Bayesin teoreema viittaa tapahtuman A ehdolliseen todennäköisyyteen, kun tapahtuma B on jo käynyt toteen. Se voidaan esittää Bayesin kaavalla muodossa $P(A|B)$, kun tapahtuman B todennäköisyys ei ole nolla:

$P(A|B)={\frac {P(B|A)\,P(A)}{P(B)}}.$

Bayesin teoreemaa voidaan käyttää Monty Hallin ongelmaan. Määritellään ensin A, K ja J, ne voivat saada arvoja joukosta $\{1,2,3\}$.

A: oven numero, minkä takana on Auto,

K: oven numero, minkä Kilpailija valitsi, ja

J: oven numero, minkä Juontaja avasi.

Koska juontaja piilottaa auton sattumanvaraisesti, kaikki oven numerot $\{1,2,3\}$ ovat yhtä todennäköisiä autolle. Tapahtuman A todennäköisyys on siis

$P(A=a)\,={\tfrac {1}{3}}$, kaikilla a:n arvoilla.

Koska kilpailijan oven valinta ei riipu auton sijainnista, tapahtumat A ja K ovat riippumattomia. Tästä seuraa, että

$P(A=a|K=k)\,=P(A=a)$, kaikilla a:n ja k:n arvoilla.

Juontajan toiminta riippuu siitä, mitkä arvot a ja k ovat saaneet:

$P(J=j\,|\,A=a,K=k)\,=\,{\begin{cases}\,\\\,\\\,\end{cases}}$	$\,0\,$		jos j = k, (juontaja ei voi avata kilpailijan valitsemaa ovea),
	$\,0\,$		jos j = a, (juontaja ei voi avata ovea, jonka takana on auto)
	$\,1/2\,$		jos j $\neq$ k ja k = a, (kahdesta muusta ovesta, joissa auto ei ole, avataan yksi sattumanvaraisesti),
	$\,1\,$		jos j $\neq$ a ja j $\neq$ k ja k $\neq$ a (on vain yksi ovi, jonka juontaja voi avata).

Kilpailija voi käyttää Bayesin teoreemaa selvittääkseen todennäköisyyden löytää auto minkä oven takaa tahansa sen jälkeen, kun kilpailija on valinnut oven ja juontaja avannut toisen:

$P(A=a|J=j,K=k)\,={\frac {P(J=j|A=a,K=k)P(A=a|K=k)}{P(J=j|K=k)}},$

missä nimittäjä muodostetaan käyttämällä kokonaistodennäköisyyden kaavaa

$P(J=j|K=k)\,=\sum _{a=1}^{3}P(J=j,A=a|K=k)=\sum _{a=1}^{3}P(J=j|A=a,K=k)P(A=a|K=k)$.

Jos esimerkiksi kilpailija valitsee alun perin oven 1, ja juontaja avaa oven 3, todennäköisyys voittaa auto vaihtamalla oveen 2 on

$P(A=2|J=3,K=1)={\frac {1\times {\frac {1}{3}}}{{\frac {1}{2}}\times {\frac {1}{3}}+1\times {\frac {1}{3}}+0\times {\frac {1}{3}}}}={\tfrac {2}{3}}.$

N ovea

Jos ovia onkin N kappaletta ja juontaja avaa p ovea, joiden takana on vuohi, niin todennäköisyys voittaa auto vaihtamalla ovea on (N−1)/[N(N−p−1)]. Jos juontaja avaa edes yhden oven, niin on todennäköisempää voittaa auto vaihtamalla ovea. Jos juontaja avaa vain yhden oven, niin oven vaihtamisen hyöty pienenee mitä suuremmaksi N kasvaa. Toisaalta, jos juontaja avaa kaikki paitsi yhden jäljellä olevista ovista, niin todennäköisyys voittaa vaihtamalla ovea kasvaa mitä suurempi N on.

Katso myös

• Kolmen vangin ongelma

Aiheesta muualla

• Selaimessa toimiva Monty-simulaatio
• Kattava kuvaus Montyn ongelmasta ja selaimessa toimiva Monty-simulaatio (englanniksi)