Hyperbolinen kulma

Hyperbolinen kulma on matematiikassa hyper­bolisen sektorin suuruutta mittaava suure. Hyper­bolinen kulma liittyy hyperbeliin hieman samaan tapaan kuin tavan­omainen kulma ympyrään.

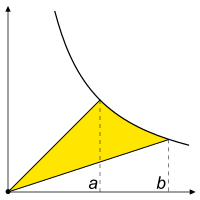
Hyperbolinen kulma on hyperbelin kaaren ja kahden origosta alkavan säteen väliseen sektoriin kulmaan liittyvä suure. Keltaisella merkitty hyperbolinen sektori on perus­asemassaan, jos a = 1.

Hyperbolinen kulma määritellään niin, että se on yhtä suuri kuin hyperbeliin xy=1 liittyvän vastaavan sektorin pinta-ala. Tämä hyperbeli on suora­kulmainen, ja sen iso­akselin puolikas on ${\sqrt {2}}$. Tämä vastaa ana­logisesti sitä, että ympyrässä, jonka säde on ${\sqrt {2}}$, on sektorin pinta-ala luku­arvoltaan sama kuin sektoria vastaava keskus­kulma.

Hyperbelille $x^{2}-y^{2}=1$ on olemassa parametriesitys:

• $x=\cosh {t}$
• $y=\sinh {t}$,

missä cosh ja sinh tarkoittavat hyper­bolisia funktiota. Näissä lausekkeissa esiintyvää parametria t sanotaan origosta pisteisiin (1, 0) ja (x, y) johtavien janojen väliseksi hyperboliseksi kulmaksi.

Määritelmä

Tarkastellaan suorakulmaista hyperbeliä $xy=1$ eli pisteiden $\textstyle \{(x,{\frac {1}{x}}):x>0\}$ uraa, ja kiinnitetään huomiota erityisesti hyperbelin siihen osaan, jossa $x>1$.

Määritellään ensin:

• Perusasennossa hyperbolinen kulma on se tasoalue, joka jää niiden puolisuorien kautta, jotka molemmat alkavat origosta ja joista toinen kulkee pisteen (1, 1), toinen taas pisteen $\textstyle (x,{\frac {1}{x}})$ kautta, missä $x>1$.
• Hyperbolisen kulma suuruudeksi määritellään vastaavan hyper­bolisen sektorin pinta-ala. Integraali­laskennan avulla voidaan osoittaa, ett tämä pinta-ala on x:n luonnollinen logaritmi ($\operatorname {ln} x$).

Tällöin voidaan todeta:

• Toisin kuin tavanomainen ympyrään liittyvä kulma, hyperbolinen kulma on ylhäältä rajoittamaton (koska $\operatorname {ln} x$ on rajoittamaton); tämä liittyy siihen, että harmonisella sarjalla ei ole ylärajaa vaan se hajaantuu.
• Kulman suuruuden lauseke viittaa siihen, että kun $0<x<1$, hyperbolinen kulma on negatiivinen. Tämä liittyy siihen, että kulma on suunnattu.

Lopuksi hyperbolisen kulman määritelmää voidaan laajentaa hyperbelin kaikkiin osiin. Olkoot $a,b,c,d$ sellaisia positiivisia reaalilukuja, että $ab=cd=1$ ja $c>a>1$, jolloin $(a,b)$ ja $(c,d)$ ovat hyperbelin $xy=1$ pisteitä ja määrittävät sille tietyn välin. Silloin kuvaus $\textstyle f:(x,y)\to (bx,ay)$, joka venyttää tai kutistaa kuviota x- tai y-akselin suunnassa, kuvaa kulman $\angle \!\left((a,b),(0,0),(c,d)\right)$ perusasemassa olevalle kulmalle $\angle \!\left((1,1),(0,0),(bc,ad)\right)$. Gregoire de Saint-Vincent todisti aikoinaan, että näiden kulmien määrittelemien hyperbolisten sektorien pinta-alat ovat yhtä suuret, ja tätä pinta-alaa sanotaan vastaavan hyperbolisen kulman suuruudeksi. Se on yhtä suuri kuin $\operatorname {ln} {(bc)}=\operatorname {ln} (c/a)=\operatorname {ln} c-\operatorname {ln} a$.

Tämä hyperbolinen kulma ei kuitenkaan ole sama kuin origosta pisteisiin (1, 0) ja (x, y) = $\cosh {t},\sinh {t})$ piirrettyjen janojen välinen tavanomaisella tavalla mitattu eli sirkulaarinen kulma. Sen sijaan jos tämä hyperbolinen kulma on t, on näiden janojen välinen tavanomaisesti mitattu kulma (radiaaneina) $\alpha =\arctan {\tanh {t}}=\arctan {\tanh {\frac {y}{x}}}$, ja kääntäen, jos tavanomaisesti mitattu kulma on $\alpha$, on näiden janojen välinen hyperbolinen kulma $t=\tanh {\operatorname {artanh} \alpha }$.

Hyperbolinen ja sirkulaarinen kulma

Yksikköhyperbeliin liittyy sektori, jonka pinta-ala on puolet hyperbolisesta kulmasta

Sirkulaarisen ja hyperbolisen kulman kasvu

Yksikköympyrään $x^{2}+y^{2}=1$ liittyy ympyräsektori, jonka pinta-ala on puolet vastaavan keskuskulman suuruudesta radiaaneina. Vastaavasti hyperbeliin $x^{2}-y^{2}=1$ liittyy hyperbolinen sektori, jonka pinta-ala on puolet hyperbolisesta kulmasta.

Projektiivisessa geometriassa ympyrän ja hyperbelin välille löytyy yhteys, sillä molemmat ovat kartioleikkauksia. Jos jommastakummasta valitaan yksi piste, muut pisteet vastaavat kulmia. Tieteellisesti keskeinen kulmien yhteenlaskua vastaamaan asetetaan seuraavalla tavalla määritelty pisteiden yhteenlasku:

Sirkulaarisia kulmia luonnehtii geometrisesti se seikka, että jos yksikköympyrään piirretään pisteestä P₀ = (1,0) alkavat jänteet P₀P₁ ja P₀P₂, joita vastaavat keskuskulmat ovat L₁ ja L₂, näiden summa L₁ + L₂ on erään sellaisen jänteen P₀Q keskuskulma, jota vastaava jana P₀Q on yhdensuuntainen janan P₁P₂ kanssa.

Hyperbelillä on vastaava ominaisuus. Jos määritellään, että P₀ = (1, 1), P₁ = (x₁, 1/x_1/ ja P₂ = (x₁, 1/x_1/), yhdensuuntaisuusehto edellyttää, että Q on piste (x₁x₂, 1/x₁1/x₂)}}. Tämän vuoksi on mielekästä määritellä origosta pisteeseen (1,1) ja mielivaltaiseen hyperbelillä olevaan pisteeseen (x, y) välinen hyperbolinen kulma tämän pisteen x-arvon logaritmisena funktiona./

Euklidisen geometrian mukaan liikuttaessa tasaisella nopeudella siten, että liikkeen suunta on aina kohtisuorassa origosta kulloinkin sijaintipisteeseen piirrettyyn säteeseen nähden, muodostuu liikerata ympyräksi. Sen sijaan pseudoeuklidisesssa avaruudessa vastaavalla tavalla liikuttaessa muodostuu ratakäyräksi hyperbeli. In Euclidean space, the multiple of a given angle traces equal distances around a circle while it traces exponential distances upon the hyperbolic line.

Sekä sirkulaarinen että hyperbolinen kulma ovat esimerkkejä invarianteista mitoista. Ympyrän kaaret, joita vastaa tietyn suuruinen keskuskulma, määrittelevät mitan eräille ympyrän kehällä muodostetuille mitallisille joukoille, eikä tämä mitta muutu ympyrän kääntyessä tai kiertyessä. Hyperbelilla tätä kääntymistä vastaa puristava kuvaus, ja hyperbolisen kulman suuruus pysyy ennallaan, kun tasoa puristetaan kuvauksella

(x, y) ↦ (rx, y / r), missä r > 0 .

Yhteys Minkowskin viiva-alkioon

Hyperbolisen kulman ja suhteellisuus­teoreettisen Minkowski-avaruuden metriikan välillä on mielen­kiintoinen yhteys. Samaan tapaan kuin kaksiulotteisessa euklidisessa geometriassa viiva-alkion pituus on

$ds_{e}^{2}=dx^{2}+dy^{2},$

vastaava pituus Minkowski-avaruudessa on

$ds_{m}^{2}=dx^{2}-dy^{2}.$

Käsitellään kaksiulotteisella euklidisella tasolla käyrää

$x=f(t),y=g(t).$,

missä parametri $t$ on reaaliluku, joka saa kaikki arvot $a$:n ja $b$:n väliltä ($a\leqslant t<b$). Tämän käyrän kaaren pituus euklidisella tasolla on

$S=\int _{a}^{b}ds_{e}=\int _{a}^{b}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}dt.$

Yhtälö $x^{2}+y^{2}=1$ määrittelee yksikköympyrän, jolla on myös yksiparametrinen esitys $x=\cos t$ ja $y=\sin t$. Rajaoittumalla väliin $0\leqslant t<\theta$ saadaan kaaren pituudeksi $S=\theta$. Jos suoritetaan muutoin sama toimenpide mutta korvataan euklidinen janaelementti Minkowskin janaelementillä,

$S=\int _{a}^{b}ds_{m}=\int _{a}^{b}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}-\left({\frac {dy}{dt}}\right)^{2}}}dt,$

ja määritellään yksikköhyperbeliksi yhtälön $y^{2}-x^{2}=1$ kuvaaja, jolla on myös parametriesitys $y=\cosh t$ ja $x=\sinh t$ sekä rajoittutaan tarkastelemaan väliä $0\leqslant t<\eta$ (hyperbolista kulmaa), todetaan, että $S=\eta$. Toisin sanoen tämä osoittaa juuri sen, että samoin kuin (sirkulaarinen) kulma voidaan määritellä yksikköympyrän kaaren pituutena euklidisessa metriikassa, voidaan hyperbolinen kulma määritellä yksikköhyperbelin kaaren Minkowskin metriikan mukaisena pituutena.

Historia

Hyperbolisen sektorin (keltaisella merkityn alueen) pinta-ala on yhtä suuri kuin hyperbelin, sen vaakasuoran asymptootin sekä pisteiden a ja b kautta kulkevan, tähän asymptoottiin nähden kohtisuorien janojen välisen alueen pinta-ala.

Hyperbelin neliöimisellä tarkoitetaan hyperbolisen sektorin pinta-alan määrittämistä. Voidaan osoittaa, että se on yhtä suuri kuin hyperbelin ja sen asymptootin välisen vastaavan alueen pinta-ala. Sen onnistui ensimmäisenä määrittämään Gregoire de Saint-Vincent vuonna 1647 teoksessaan Opus geometricum quadrature circuli et sectionum coni. Kuten eräs historioitsija myöhemmin asian ilmaisi, Saint-Vincent neliöi hyperbelin ja sen asymptoottien välisen alueen ja totesi, että tämän alueen pinta-ala kasvoi aritmeettisen sarjan mukaan samalla kun abskissa kasvoi geometrisen sarjan mukaan.

A. A. de Sarasa määritteli luonnollisen logaritmin hyperbelin avulla. Tämän määritelmän mukaan luvun a luonnollinen eli "hyperbolinen logaritmi" on hyperberlin $y=1/x$, x-akselin sekä suorien x=1 ja x=a välisen alueen pinta-ala. Tämä funktio, joka on tunnetuimpia esimerkkejä transkendenttisesta funktiosta, voidaan kuitenkin yhtäpitävästi määritellä toisinkin, nimittäin eksponenttifunktion $e^{x}$ käänteisfunktiona. Hyperbolisella kulmalla on kuitenkin keskeinen merkitys, kun Saint-Vincentin lauseen pohjalta on kehitetty puristuskuvausten teoria.

Ympyrän trigonometrian yleisti hyperbelille Augustus De Morgan vuonna 1849 laatimassaan oppikirjassa Trigonometry and Double Algebra. Vuonna 1878 W. K. Clifford parametrisoi hyperbolisen kulman avulla yksikköhyperbelin kuvaillen sitä kvasiharmonisena liikkeenä.

Vuonna 1894 Alexander Macfarlane julkaisi teoksessaan Papers on Space Analysis tutkielman The Imaginary of Algebra, jossa hän generoi hyperbolisten kulmien avulla hyperboliset versorit. Seuraavana vuonna Bulletin of the American Mathematical Society julkaisi Mellen W. Haskelin tutkielman hyperbolisista funktioista.

Vuonna 1914 laatimassaan suhteellisuusteorian oppikirjassa Ludwik Silberstein käytti rapiditeetin käsittettä ja osoittin sen yhteyden hyperbolisen avaruuden kolmioihin. Rapiditeetti määriteltiin hyperbolisena kulmana $a=\tanh {\frac {v}{c}}$, toisin sanoen kappaleen nopeuden ja valon­nopeuden suhteen hyperbolisena tangenttina. Hän kirjoitti:

"On syytä huomauttaa, että rapiditeetin arvo 1 vastaa jo huimaa nopeutta, noin kolmea neljäsosaa valonnopeudesta; tarkemmin sanottuna v = 0,7616c, kuna=1." "Niinpä rapiditeetti a=1 merkitsee nopeutta 0,76 c, mikä on hieman suurempi kuin valon nopeus vedessä."

Silberstein käytti myös Nikolai Lobatševskin esittämää parallelismikulman käsitettä Π(a), jolla saatiin $\Pi (a)={\frac {v}{c}}$.

Hyperbolinen kulma imaginaarisena kulmana

Hyperbolinen kulma esitetään usein ikään kuin se olisi imaginaariluku. Jos x on mikä tahansa reaaliluku, pätee trigonometristen ja hyperbolisten funktioiden välillä yhteys

$\cos(ix)=\cosh(x)\quad {\text{ja}}\quad \sin(ix)=i\sinh(x)$,

joten hyperboliset funktiot cosh ja sinh voidaan esittää sirkulaaristen, trigonometristen funktioiden avulla. Nämä yhteydet eivät kuitenkaan suoranaisesti ilmene ympyrässä tai rotaatiossa, mitenkään, vaan ne on paremmin ymmärrettävissä päättymättömien sarjojen käsittein. Erityisesti eksponenttifunktiota ($e^{x}=\cosh x+\sinh x\!$ ) esittävä sarja muodostuu parillisista ja parittomista termeistä, joista edelliset muodostavat hyperbolisen kosinifunktion ($\textstyle \cosh x=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}$), jälkimmäiset hyperbolisen sinifunktion ($\textstyle \sinh x=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}$). Kosinia vastaava päättymätön sarja voidaan muodostaa funktion cosh sarjasta korvaamalla sen joka toinen termi vasta­luvullaan eli muuttamalla se vuorottelevaksi, ja vastaavalla tavalla saadaan sinifunktion sarja funktion sinh sarjasta. Tämä voidaan tehdä kertomalla sarjan jokainen termi vuorottelutekijällä (−1)ⁿ. Edellä olevat funktioiden väliset yhteydet saadaan korvaamalla tämä vuorottelutekijä imaginaari­yksiköllä i, jolloin saadaan palautetuksi eksponentti­funktion sarjan molemmat osasarjat. Kuitenkin holomorfisten funktioiden teoriassa hyperbolisia sini- ja kosinifunktioita käsitellään kompleksisina sini- ja kosinifunktioina.

Aiheesta muualla

• William Mueller: ”The number e: Example 5: Hyperbolic Trigonometry”, Exloring Precalculus. {{{Julkaisija}}}. Teoksen verkkoversio.

• {{verkkoviite | Osoite = https://en.wikibooks.org/wiki/Calculus/Hyperbolic_angle | Nimeke = Calculus / Hyperbolic angle | Sivusto = WikiBooks |